LeetCode + 《剑指Offer II》刷题笔记。

动态规划

1D DP

70 Climbing Stairs

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n+1);
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int climbStairs(int n) {
        int first=1,second=1,third;
        for(int i=2;i<=n;i++){
            third=first+second;
            first=second;
            second=third;
        }
        return second;
    }
};

注意这里return的是second，如果n为1应该返回1，所以最后返回second。

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

322 Coin Change

Greedy doesn’t work

DFS-Backtracking

一般DFS涉及到Backtracking以decision tree的方式思考更容易理解。

top-down: recursive dfs, for amount, branch for each coin, cache to store prev coin_count for each amount;

Dynamic Programming

bottom-up: compute coins for amount = 1, up until n, using for each coin (amount - coin), cache prev values

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,amount+1);
        dp[0]=0;
        for(int i=1;i<=amount;i++){
            for(int coin:coins){
                if(i-coin>=0){
                    dp[i]=min(dp[i],1+dp[i-coin]);
                }
            }
        }
        return dp[amount]==amount+1?-1:dp[amount];
    }
};
  • 时间复杂度：O(amount*length(coins))
  • 空间复杂度：O(amount)

300 Longest Increasing Subsequence

Brute Force-DFS

300-brute-force

  • 时间复杂度：O(2^n)

DFS-With Cache

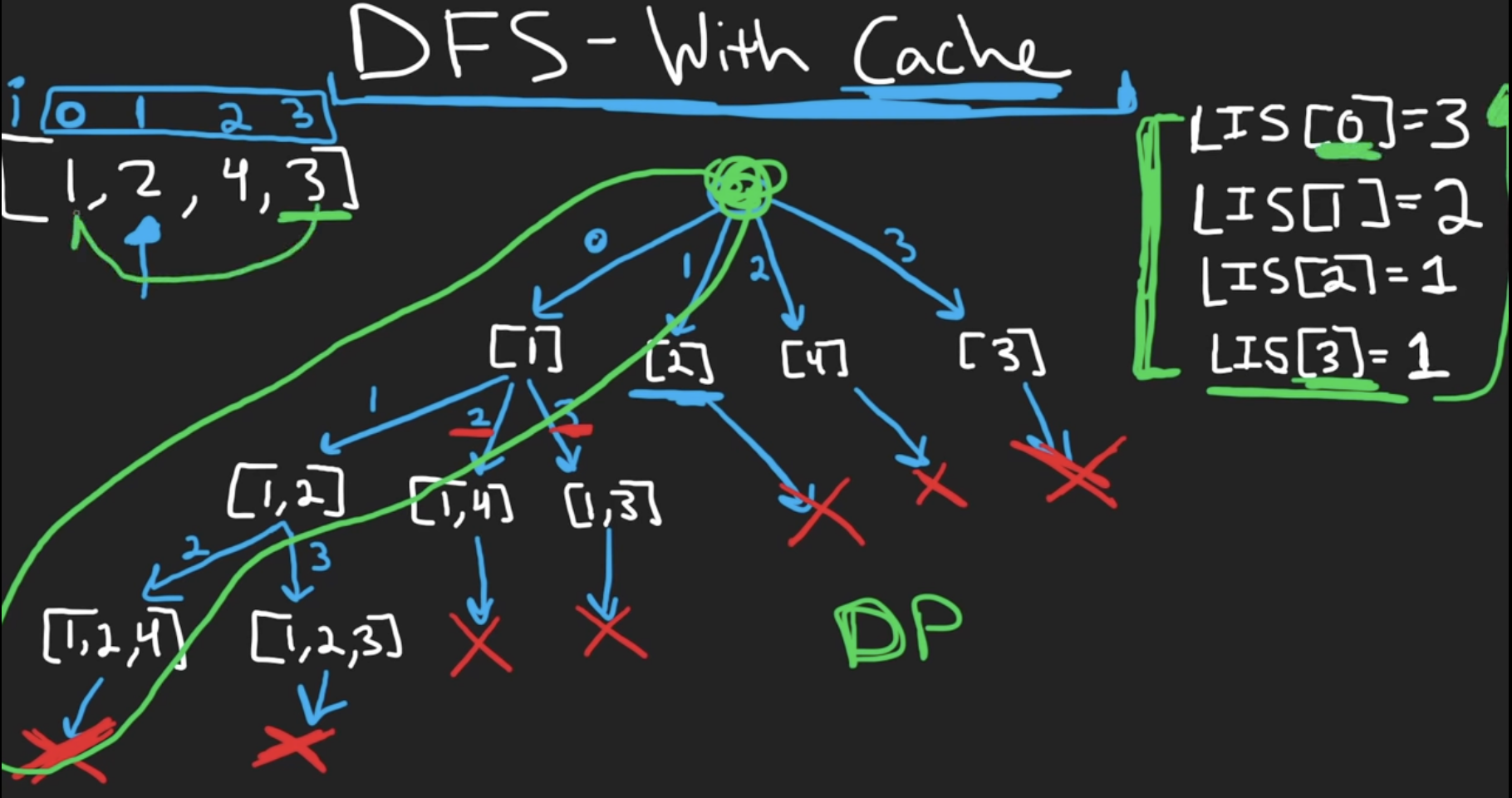
300-dfs

Dynamic Programming

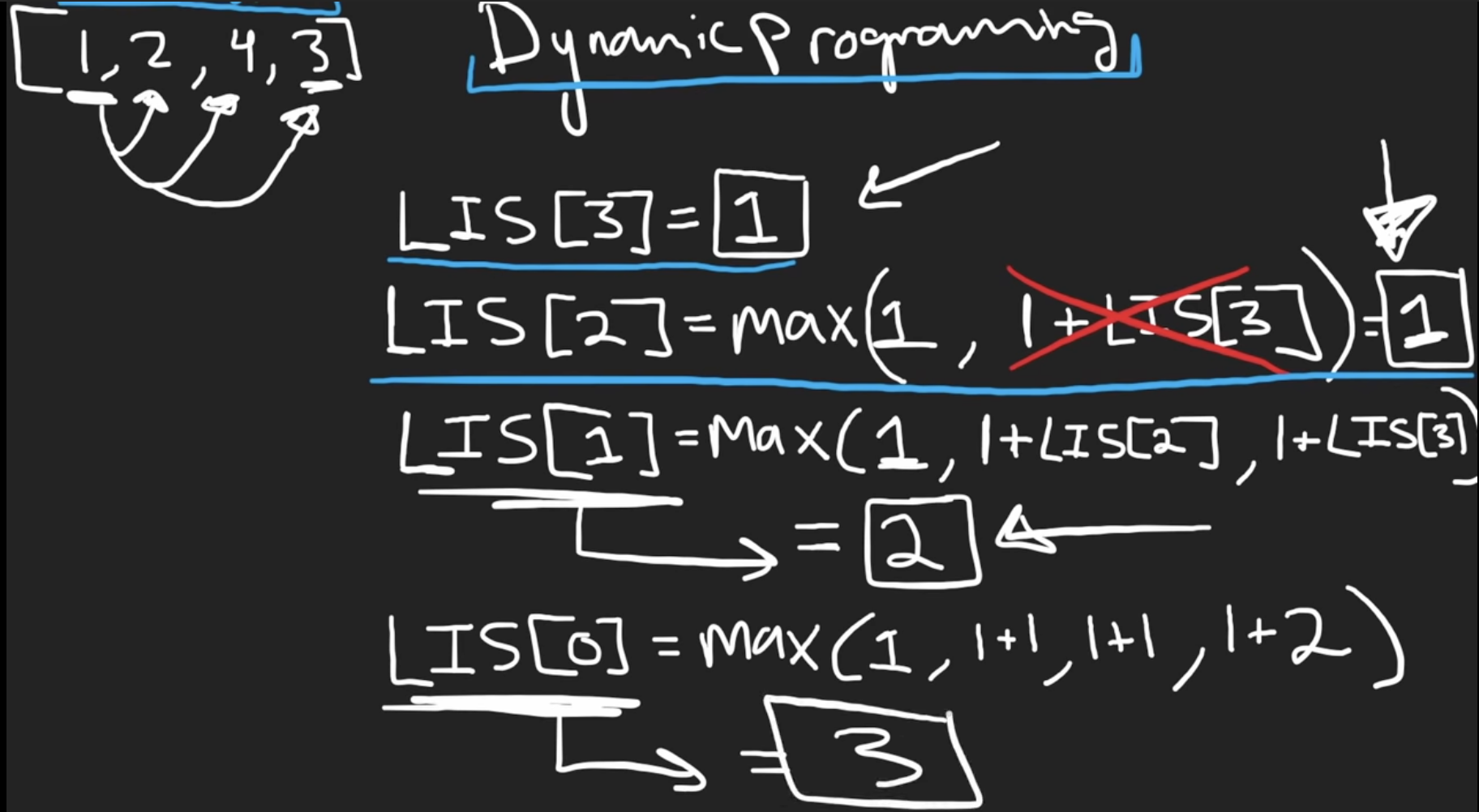
300-dp

longest increasing subsequence starting at each index

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        //longest increasing subsequence starting at each index
        vector<int> LIS(n,1);
        for(int i=n-1;i>=0;i--){
            for(int j=i+1;j<n;j++){
                if(nums[i]<nums[j]){
                    LIS[i]=max(LIS[i],1+LIS[j]);
                }
            }
        }
        return *max_element(LIS.begin(),LIS.end());
    }
};

  • 时间复杂度：O(n^2)

  • 空间复杂度：O(n)

longest increasing subsequence ending at each index

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        //longest increasing subsequence ending at each index
        vector<int> LIS(n,1);
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]){
                    LIS[i]=max(LIS[i],1+LIS[j]);
                }
            }
        }
        return *max_element(LIS.begin(),LIS.end());
    }
};

  • 时间复杂度：O(n^2)

  • 空间复杂度：O(n)
  • 时间复杂度：O(nlogn)
  • 空间复杂度：O(n)

746 Min Cost Climbing Stairs

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        vector<int> dp(n+1,0);
        for(int i=2;i<=n;i++){
            dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[n];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        int prev=0,cur=0,next;
        for(int i=2;i<=n;i++){
            next=min(cur+cost[i-1],prev+cost[i-2]);
            prev=cur;
            cur=next;
        }
        return cur;
    }
};

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

139 Word Break

for each prefix, if prefix is in dict and wordbreak(remaining str)=True, then return True, cache result of wordbreak;

instead of checking every single possible prefix right of any length what we’re going to be doing is we’re going to be checking every single word in wordDict as the prefix.

Decision Tree——Cache——DP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        int sLen=s.length();
        vector<bool> dp(sLen+1,false);
        dp[sLen]=true;
        for(int i=sLen-1;i>=0;i--){
            for(string word:wordDict){
                int wordLen=word.length();
                //substr(pos,n)
                if(i+wordLen<=sLen && word==s.substr(i,wordLen)){
                    dp[i]=dp[i+wordLen];
                }
                if(dp[i]){
                    break;
                }
            }
        }
        return dp[0];
    }
};

  • 时间复杂度：O(length(s)*size(wordDict))

  • 空间复杂度：O(length(s))

198 House Robber

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int rob(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return nums[0];
        vector<int> dp(n);
        dp[0]=nums[0];
        dp[1]=max(nums[0],nums[1]);
        for(int i=2;i<n;i++){
            dp[i]=max(nums[i]+dp[i-2],dp[i-1]);
        }
        return dp[n-1];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int rob(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return nums[0];
        int prev=nums[0];
        int cur=max(nums[0],nums[1]);
        int next;
        for(int i=2;i<n;i++){
            next=max(nums[i]+prev,cur);
            prev=cur;
            cur=next;
        }
        return cur;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

213 House Robber II

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int rob(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return nums[0];
        if(n==2) return max(nums[0],nums[1]);
        return max(robRange(nums,0,n-2),robRange(nums,1,n-1));
    }
    int robRange(vector<int>& nums,int left,int right){
        int n=nums.size();
        vector<int> dp(n);
        dp[left]=nums[left];
        dp[left+1]=max(nums[left],nums[left+1]);
        for(int i=left+2;i<=right;i++){
            dp[i]=max(nums[i]+dp[i-2],dp[i-1]);
        }
        return dp[right];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
public:
    int rob(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return nums[0];
        if(n==2) return max(nums[0],nums[1]);
        return max(robRange(nums,0,n-2),robRange(nums,1,n-1));
    }
    int robRange(vector<int>& nums,int left,int right){
        int prev=nums[left];
        int cur=max(nums[left],nums[left+1]);
        int next;
        for(int i=left+2;i<=right;i++){
            next=max(nums[i]+prev,cur);
            prev=cur;
            cur=next;
        }
        return cur;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

91 Decode Ways

LINK: FACEBOOK CODING INTERVIEW QUESTION - DECODE WAYS (LeetCode)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int numDecodings(string s) {
        int len=s.length();
        vector<int> dp(len+1);
        dp[0]=1;
        dp[1]=(s[0]=='0'?0:1);
        for(int i=2;i<=len;i++){
            int oneDigit=s[i-1]-'0';
            int twoDigit=stoi(s.substr(i-2,2));
            if(oneDigit!=0) dp[i]+=dp[i-1];
            if(twoDigit>=10 && twoDigit<=26) dp[i]+=dp[i-2];
        }
        return dp[len];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int numDecodings(string s) {
        int len=s.length();
        vector<int> dp(len+1);
        int prev=1;
        int cur=(s[0]=='0'?0:1);
        for(int i=2;i<=len;i++){
            int next=0;
            int oneDigit=s[i-1]-'0';
            int twoDigit=stoi(s.substr(i-2,2));
            if(oneDigit!=0) next+=cur;
            if(twoDigit>=10 && twoDigit<=26) next+=prev;
            prev=cur;
            cur=next;
        }
        return cur;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int numDecodings(string s) {
        int len=s.length();
        vector<int> dp(len+1);
        dp[0]=1;
        for(int i=1;i<=len;i++){
            if(s[i-1]!='0') dp[i]+=dp[i-1];
            if(i>=2){
                int twoDigit=stoi(s.substr(i-2,2));
                if(twoDigit>=10 && twoDigit<=26) dp[i]+=dp[i-2];
            }
        }
        return dp[len];
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

55 Jump Game

Dynamic Programming
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

Greedy

从前往后

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n=nums.size();
        int rightMost=0;
        for(int i=0;i<n;i++){
            if(i<=rightMost){
                rightMost=max(rightMost,i+nums[i]);
                if(rightMost>=n-1){
                    return true;
                }
            }
        }
        return false;
    }
};

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

从后往前

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n=nums.size();
        int goal=n-1;
        for(int i=n-1;i>=0;i--){
            if(i+nums[i]>=goal){
                goal=i;
            }
        }
        return goal==0?true:false;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

5 Longest Palindromic Substring

DP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n<2) return s;
        vector<vector<bool>> dp(n,vector<bool>(n,false));
        for(int i=0;i<n;i++){
            dp[i][i]=true;
        }
        int begin=0;
        int maxLen=1;
        for(int L=2;L<=n;L++){
            for(int i=0;i<n;i++){
                int j=i+L-1;
                if(j>=n) break;
                if(s[i]==s[j]){
                    if(j-i<=2){
                        dp[i][j]=true;
                    }else{
                        dp[i][j]=dp[i+1][j-1];
                    }
                }else{
                    dp[i][j]=false;
                }
                if(j-i+1>maxLen && dp[i][j]){
                    begin=i;
                    maxLen=j-i+1;
                }
            }
        }
        return s.substr(begin,maxLen);
    }
};
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(n^2)

中心拓展算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n<=1) return s;
        int left=0,right=0;
        int len=1;
        int maxStart=0;
        int maxLen=0;
        for(int i=0;i<n;i++){
            left=i-1;
            right=i+1;
            while(left>=0 && s[left]==s[i]){
                len+=1;
                left--;
            }
            while(right<n && s[right]==s[i]){
                len+=1;
                right++;
            }
            while(left>=0 && right<n && s[left]==s[right]){
                len+=2;
                left--;
                right++;
            }
            if(len>maxLen){
                maxStart=left;
                maxLen=len;
            }
            len=1;
        }
        return s.substr(maxStart+1,maxLen);
    }
};
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

343 整数拆分

递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int integerBreak(int n) {
        if(n==1 || n==2){
            return 1;
        }
        int res=0;
        for(int i=1;i<=n;i++){
            res=max({res,i*integerBreak(n-i),i*(n-i)});
        }
        return res;
    }
};

超出时间限制。

DP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n+1);
        for(int i=2;i<=n;i++){
            for(int j=1;j<i;j++){
                dp[i]=max({dp[i],j*dp[i-j],j*(i-j)});
            }
        }
        return dp[n];
    }
};
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(n)

2D DP

1143 Longest Common Subsequence

Buttom-Up1

recursive: if first chars are equal find lcs of remaining of each, else max of: lcs of first and remain of 2nd and lcs of 2nd remain of first, cache result; nested forloop to compute the cache without recursion;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.length(),n=text2.length();
        vector<vector<int>> LCS(m+1,vector<int>(n+1));
        // for(int i=0;i<=m;i++){
        //     LCS[i][n]=0;
        // }
        // for(int j=0;j<=n;j++){
        //     LCS[m][j]=0;
        // }
        for(int i=m-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                if(text1[i]==text2[j]){
                    LCS[i][j]=1+LCS[i+1][j+1];
                }else{
                    LCS[i][j]=max(LCS[i+1][j],LCS[i][j+1]);
                }
            }
        }
        return LCS[0][0];
    }
};

注意：这里比较的是text1[i]==text2[j]

  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)

Buttom-Up2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.length(),n=text2.length();
        vector<vector<int>> LCS(m+1,vector<int>(n+1));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(text1[i-1]==text2[j-1]){
                    LCS[i][j]=1+LCS[i-1][j-1];
                }else{
                    LCS[i][j]=max(LCS[i-1][j],LCS[i][j-1]);
                }
            }
        }
        return LCS[m][n];
    }
};

注意：这里比较的是text1[i-1]==text2[j-1]

  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)

62 Unique Paths

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m,vector<int>(n,1));
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> pre(n,1),cur(n,1);
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                cur[j]=pre[j]+cur[j-1];
            }
            pre=cur;
        }
        return cur[n-1];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(2*n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> dp(n,1);
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[j]+=dp[j-1];
            }
        }
        return dp[n-1];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(n)

97 Interleaving String

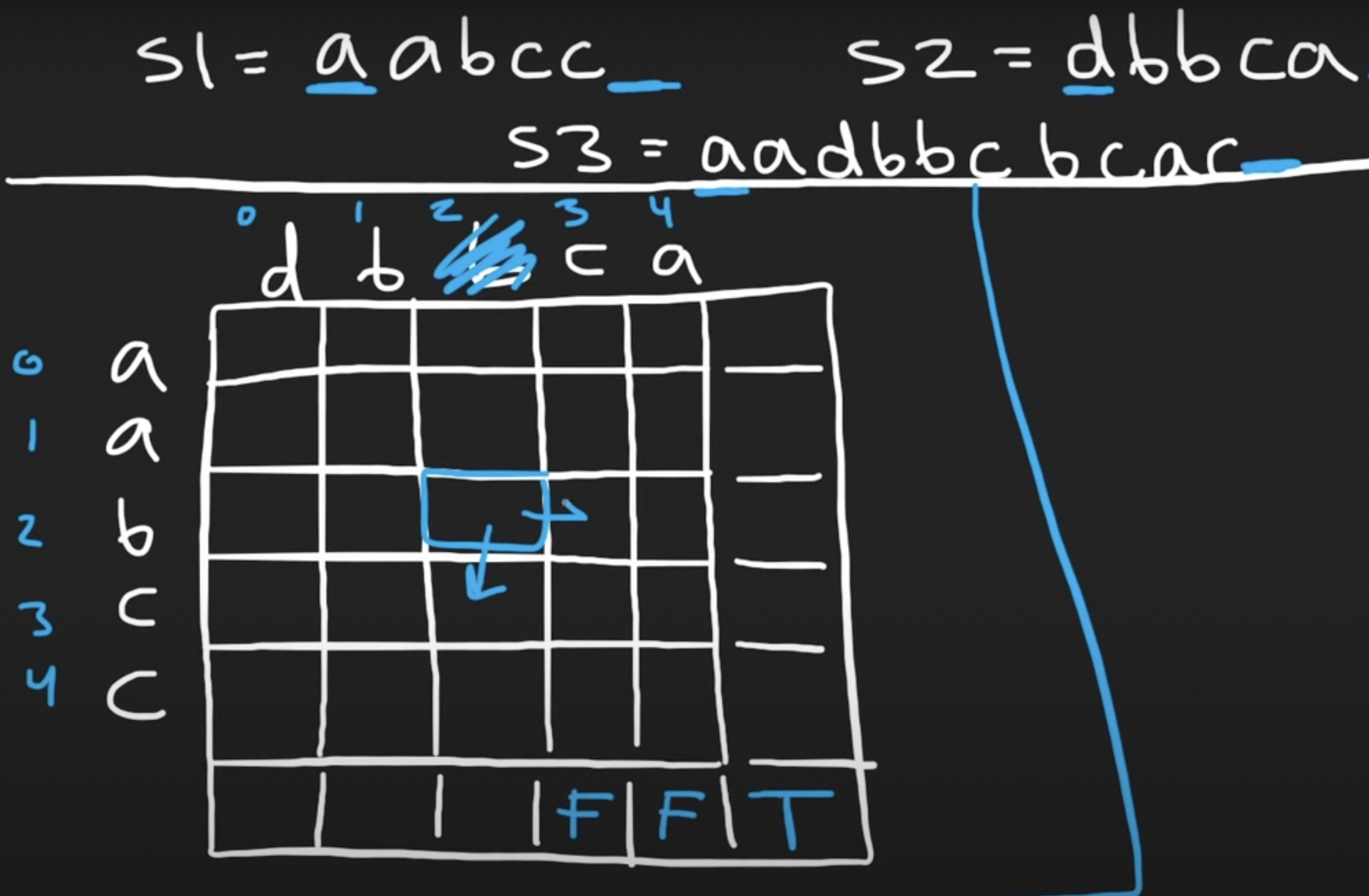
leetcode-97

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int len1=s1.length(),len2=s2.length();
        if(len1+len2!=s3.length()) return false;
        vector<vector<bool>> dp(len1+1,vector<bool>(len2+1,false));
        dp[len1][len2]=true;
        for(int i=len1;i>=0;i--){
            for(int j=len2;j>=0;j--){
                if(i<len1 && s1[i]==s3[i+j] && dp[i+1][j]){
                    dp[i][j]=true;
                }
                if(j<len2 && s2[j]==s3[i+j] && dp[i][j+1]){
                    dp[i][j]=true;
                }
            }
        }
        return dp[0][0];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)

1155 Number of Dice Rolls With Target Sum

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    const int MOD=1e9+7;
    int numRollsToTarget(int n, int k, int target) {
        //dp[i][j] 扔i枚骰子和为j
        vector<vector<int>> dp(n+1,vector<int>(target+1,0));
        dp[0][0]=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=target;j++){
                for(int t=1;t<=k;t++){
                    if(t<=j){
                        dp[i][j]=(dp[i][j]+dp[i-1][j-t])%MOD;
                    }
                }
            }
        }
        return dp[n][target];
    }
};
  • 时间复杂度：O(n*target*k)
  • 空间复杂度：O(n*target)

64 Minimum Path Sum

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n));
        dp[0][0]=grid[0][0];
        for(int i=1;i<m;i++){
            dp[i][0]=dp[i-1][0]+grid[i][0];
        }
        for(int j=1;j<n;j++){
            dp[0][j]=dp[0][j-1]+grid[0][j];
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)

801 Minimum Swaps To Make Sequences Increasing

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
public:
    int minSwap(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size();
        vector<vector<int>> dp(n,vector<int>(2));
        dp[0][0]=0;
        dp[0][1]=1;
        //其余未知状态初始化为正无穷
        for(int i=1;i<n;i++){
            dp[i][0]=dp[i][1]=n+10;
        }
        for(int i=1;i<n;i++){
            if(nums1[i]>nums1[i-1] && nums2[i]>nums2[i-1]){
                //都不交换
                dp[i][0]=dp[i-1][0];
                //都交换
                dp[i][1]=dp[i-1][1]+1;
            }
            if(nums1[i]>nums2[i-1] && nums2[i]>nums1[i-1]){
                //当前位置 i 和前一位置 i - 1 只能有其一发生交换
                //前一位置交换
                dp[i][0]=min(dp[i][0],dp[i-1][1]);
                //当前位置交换
                dp[i][1]=min(dp[i][1],dp[i-1][0]+1);
            }
        }
        return min(dp[n-1][0],dp[n-1][1]);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
public:
    int minSwap(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size();
        vector<vector<int>> dp(2,vector<int>(2));
        dp[0][0]=0;
        dp[0][1]=1;
        for(int i=1;i<n;i++){
            int a=n+10,b=n+10;
            int prev=(i-1)&1,cur=i&1;
            if(nums1[i]>nums1[i-1] && nums2[i]>nums2[i-1]){
                //都不交换
                a=dp[prev][0];
                //都交换
                b=dp[prev][1]+1;
            }
            if(nums1[i]>nums2[i-1] && nums2[i]>nums1[i-1]){
                //当前位置 i 和前一位置 i - 1 只能有其一发生交换
                //前一位置交换
                a=min(a,dp[prev][1]);
                //当前位置交换
                b=min(b,dp[prev][0]+1);
            }
            dp[cur][0]=a;
            dp[cur][1]=b;
        }
        return min(dp[(n-1)&1][0],dp[(n-1)&1][1]);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

10 Regular Expression Matching

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.size();
        int n=p.size();
        auto matches=[&](int i,int j){
            if(i==0) return false;
            if(p[j-1]=='.') return true;
            return s[i-1]==p[j-1];
        };
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        dp[0][0]=1;
        for(int i=0;i<=m;i++){
            for(int j=1;j<=n;j++){
                if (p[j - 1] == '*') {
                    dp[i][j] |= dp[i][j - 2];
                    if (matches(i, j - 1)) {
                        dp[i][j] |= dp[i - 1][j];
                    }
                }
                else {
                    if (matches(i, j)) {
                        dp[i][j] |= dp[i - 1][j - 1];
                    }
                }
            }
        }
        return dp[m][n];
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(mn)

115 Distinct Subsequences
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

940 Distinct Subsequences II
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)