LeetCode + 《剑指Offer II》刷题笔记。

图

图的搜索

如果要求在无权图中找出两个节点之间的最短距离，那么广度优先搜索可能是更合适的算法。

如果面试题要求找出符合条件的路径，那么深度优先搜索可能是更合适的算法。

避免死循环的办法是记录已经搜索过的节点，在访问一个节点之前先判断该节点之前是否已经访问过，如果之前访问过那么这次就略过不再重复访问。

假设一个图有v个节点、e条边。不管是采用BFS还是DFS，每个节点都只会访问一次，并且会沿着每条边判断与某个节点相邻的节点是否已经访问过，因此时间复杂度是O（v+e）。

695 Max Area of Island

思路：

获得网格中每个连通形状的面积，然后取最大值。
如果在一个土地上，以 4 个方向探索与之相连的每一个土地（以及与这些土地相连的土地），那么探索过的土地总数将是该连通形状的面积。
为了确保每个土地访问不超过一次，每次经过一块土地时，将这块土地的值置为 0。这样就不会多次访问同一土地，同时也没有使用visited变量的额外空间。

DFS(Recursive)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        int maxArea=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==1){
                    int area=dfs(grid,i,j);
                    maxArea=max(maxArea,area);
                }
            }
        }
        return maxArea;
    }
    int dfs(vector<vector<int>>& grid,int i,int j){
        if(i<0 || i==grid.size() || j<0 || j==grid[0].size() || grid[i][j]==0){
            return 0;
        }
        int area=1;
        grid[i][j]=0;
        int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
        for(int k=0;k<4;k++){
            int x=i+dir[k][0];
            int y=j+dir[k][1];
            area+=dfs(grid,x,y);
        }
        return area;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

DFS(Stack)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m=grid.size(),n=grid[0].size();
        int maxArea=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==1){
                    int area=getArea(grid,i,j);
                    maxArea=max(maxArea,area);
                }
            }
        }
        return maxArea;
    }
    int getArea(vector<vector<int>>& grid,int i,int j){
        stack<vector<int>> stk;
        int area=0;
        stk.push(vector{i,j});
        int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
        while(!stk.empty()){
            vector<int> cur=stk.top();
            stk.pop();
            int curi=cur[0],curj=cur[1];
            if(curi<0 || curi==grid.size() || curj<0 || curj==grid[0].size() 
               || grid[curi][curj]!=1){
                continue;
            }
            area+=1;
            grid[curi][curj]=0;
            for(int k=0;k<4;k++){
                int nextx=curi+dir[k][0];
                int nexty=curj+dir[k][1];
                stk.push(vector{nextx,nexty});
            }
        }
        return area;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m=grid.size(),n=grid[0].size();
        int maxArea=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==1){
                    int area=getArea(grid,i,j);
                    maxArea=max(maxArea,area);
                }
            }
        }
        return maxArea;
    }
    int getArea(vector<vector<int>>& grid,int i,int j){
        queue<int> qi;
        queue<int> qj;
        qi.push(i);
        qj.push(j);
        int area=0;
        int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
        while(!qi.empty()){
            int curi=qi.front();
            int curj=qj.front();
            qi.pop();
            qj.pop();
            if(curi<0 || curi==grid.size() || curj<0 || curj==grid[0].size() 
               || grid[curi][curj]!=1){
                continue;
            }
            area+=1;
            grid[curi][curj]=0;
            for(int k=0;k<4;k++){
                int nexti=curi+dir[k][0];
                int nextj=curj+dir[k][1];
                qi.push(nexti);
                qj.push(nextj);
            }
        }
        return area;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

785 Is Graph Bipartite?

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        //colors:0未着色 1/-1两种不同的颜色 1条edge的相邻node着色为-color
        int n=graph.size();
        vector<int> colors(n);
        for(int i=0;i<n;i++){
            if(colors[i]==0){
                if(!dfs(graph,colors,i,1)){
                    return false;
                }
            }
        }
        return true;
    }
    bool dfs(vector<vector<int>>& graph,vector<int>& colors,int i,int color){
        if(colors[i]!=0){
            return colors[i]==color;
        }
        colors[i]=color;
        for(int neighbor:graph[i]){
            if(!dfs(graph,colors,neighbor,-color)){
                return false;
            }
        }
        return true;
    }
};

时间复杂度：O(v+e)
空间复杂度：O(n)，存储节点颜色的数组需要 O(n) 的空间，DFS栈的深度最大为 n，需要 O(n)的空间。

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        //colors:0未着色 1/-1两种不同的颜色 1条edge的相邻node着色为-color
        int n=graph.size();
        vector<int> colors(n);
        for(int i=0;i<n;i++){
            if(colors[i]==0){
                if(!bfs(graph,colors,i,1)){
                    return false;
                }
            }
        }
        return true;
    }
    bool bfs(vector<vector<int>>& graph,vector<int>& colors,int i,int color){
        queue<int> q;
        q.push(i);
        colors[i]=color;
        while(!q.empty()){
            int cur=q.front();
            q.pop();
            for(int neighbor:graph[cur]){
                if(colors[neighbor]!=0){
                    if(colors[neighbor]==colors[cur]) return false;
                }else{
                    q.push(neighbor);
                    colors[neighbor]=(-colors[cur]);
                }
            }
        }
        return true;
    }
};

时间复杂度：O(v+e)
空间复杂度：O(n)

542 01 Matrix

应用与图相关的算法解决问题的前提是能够找出图中的节点和边。这是一个背景为矩阵的问题，矩阵中的每个格子可以看成图中的一个节点，矩阵中上、下、左、右相邻的格子对应的节点之间有一条边相连。

可以将图看成一个无权图，图中两个节点的距离是连通它们的路径经过的边的数目。由于这个问题与无权图的最近距离相关，因此可以考虑应用广度优先搜索解决。

这个问题是求每个格子离最近的0的距离，因此可以将所有的0当作初始节点添加到队列中，然后以值为0的节点作为起点做广度优先搜索。如果经过d步到达某个格子，那么该格子离最近的0的距离就是d。

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m=mat.size(),n=mat[0].size();
        queue<vector<int>> q;
        vector<vector<int>> res(m,vector<int>(n));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(mat[i][j]==0){
                    res[i][j]=0;
                    q.push(vector{i,j});
                }else{
                    res[i][j]=INT_MAX;
                }
            }
        }
        //bfs
        int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
        while(!q.empty()){
            vector<int> cur=q.front();
            q.pop();
            int i=cur[0],j=cur[1];
            int dis=res[i][j];
            for(int k=0;k<4;k++){
                int x=i+dir[k][0];
                int y=j+dir[k][1];
                if(x<0 || x==mat.size() || y<0 || y==mat[0].size()){
                    continue;
                }
                if(dis+1<res[x][y]){
                    res[x][y]=dis+1;
                    q.push(vector{x,y});
                }
            }
        }
        return res;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

752 Open the Lock

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


class Solution {
public:
    vector<string> getNeighbors(string s){
        vector<string> res;
        for(int i=0;i<4;i++){
            char temp=s[i];
            //注意，这里是temp，debug了好久！
            s[i]=(temp=='0'?'9':temp-1);
            res.push_back(s);
            s[i]=(temp=='9'?'0':temp+1);
            res.push_back(s);
            s[i]=temp;
        }
        return res;
    }
    int openLock(vector<string>& deadends, string target) {
        if(target=="0000") return 0;

        unordered_set<string> dead(deadends.begin(),deadends.end());
        string init="0000";
        if(dead.count(target) || dead.count(init)) return -1;

        queue<pair<string,int>> q;
        q.emplace(init,0);
        unordered_set<string> visited={init};
        while(!q.empty()){
            auto [cur,step]=q.front();
            q.pop();
            for(string next:getNeighbors(cur)){
                if(!dead.count(next) && !visited.count(next)){
                    if(next==target) return step+1;
                    q.emplace(next,step+1);
                    visited.insert(next);
                }
            }
        }
        return -1;
    }
};

时间复杂度：O(10^4)
空间复杂度：O(n)

797 All Paths From Source to Target

本题中的图为有向无环图（DAG: directed acyclic graph），搜索过程中不会反复遍历同一个点，因此无需判断当前点是否遍历过。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> paths;
        vector<int> path;
        dfs(graph,paths,path,0);
        return paths;
    }
    void dfs(vector<vector<int>>& graph,vector<vector<int>>& paths,vector<int>& path,int start){
        path.push_back(start);
        if(start==graph.size()-1){
            paths.push_back(path);
        }else{
            for(int next:graph[start]){
                dfs(graph,paths,path,next);
            }
        }
        path.pop_back();
    }
};

时间复杂度：O(v+e)
空间复杂度：O(n)

399 Evaluate Division

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


class Solution {
public:
    unordered_map<string,unordered_map<string,double>> mp;
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        for(int i=0;i<equations.size();i++){
            string a=equations[i][0],b=equations[i][1];
            mp[a][b]=values[i];
            mp[b][a]=1.0/values[i];
        }
        vector<double> res;
        vector<string> visited;
        for(vector<string> query:queries){
            string a=query[0],b=query[1];
            if(mp[a].size()==0 || mp[b].size()==0){
                res.push_back(-1.0);
            }else{
                unordered_set<string> visited;
                res.push_back(dfs(a,b,visited));
            }
        }
        return res;
    }
    double dfs(string from,string to,unordered_set<string>& visited){
        if(from==to){
            return 1.0;
        }
        visited.insert(from);
        unordered_map<string,double> temp=mp[from];
        for(auto it=temp.begin();it!=temp.end();it++){
            if(!visited.count(it->first)){
                double nextValue=dfs(it->first,to,visited);
                //要有nextValue的判断：因为有可能返回-1.0
                if(nextValue>0){
                    return it->second*nextValue;
                }
            }
        }
        visited.erase(from);
        return -1.0;
    }
};

时间复杂度：O(v+e)
空间复杂度：O(v+e)

329 Longest Increasing Path in a Matrix

记忆化DFS

由于这个问题是关于递增路径的，因此只关心从较小的数字指向较大的数字的边，两个不同数字在图中对应的节点之间的边是有向边，针对这个问题构建出来的图是一个有向图。同时，由于图中所有边都是从较小的数字指向较大的数字，这样的边不可能形成环，因此构建出来的图一定是有向无环图DAG。

以矩阵中某个坐标为起点的最长递增路径的长度至少是1。如果“lengths[i][j]”的值大于0，就说明之前已经计算过以坐标（i，j）为起点的最长递增路径的长度，如果在计算以其他坐标为起点的最长递增路径的长度时需要以坐标（i，j）为起点的最长递增路径的长度，就没有必要再次计算，只需要直接返回就可以。矩阵lengths在这里还起到了缓存的作用，能够确保以任意坐标为起点的最长递增路径的长度只需要计算一次。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int m=matrix.size(),n=matrix[0].size();
        if(m==0 || n==0){
            return 0;
        }
        int longest=0;
        //memo[i][j]保存的是从矩阵中（i，j）出发的最长递增路径的长度
        vector<vector<int>> memo(m,vector<int>(n));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                longest=max(longest,dfs(matrix,memo,i,j));
            }
        }
        return longest;
    }
    int dfs(vector<vector<int>>& matrix,vector<vector<int>>& memo,int i,int j){
        if(memo[i][j]!=0){
            return memo[i][j];
        }
        int m=matrix.size(),n=matrix[0].size();
        vector<vector<int>> temp={{-1,0},{1,0},{0,-1},{0,1}};
        memo[i][j]++;
        for(vector<int> t:temp){
            int row=i+t[0];
            int column=j+t[1];
            if(row>=0 && row<m && column>=0 && column<n && matrix[row][column]>matrix[i][j]){
                memo[i][j]=max(memo[i][j],dfs(matrix,memo,row,column)+1);
            };
        }
        return memo[i][j];
    }
};

时间复杂度：O(mn)，DFS为O(v+e)，O(v)=O(mn)，O(e)=O(4mn)=O(mn)
空间复杂度：O(mn)

417 Pacific Atlantic Water Flow

如果直接以每个单元格作为起点模拟雨水的流动，则会重复遍历每个单元格，导致时间复杂度过高。为了降低时间复杂度，可以从矩阵的边界开始反向搜索寻找雨水流向边界的单元格，反向搜索时，每次只能移动到高度相同或更大的单元格。

由于矩阵的左边界和上边界是太平洋，矩阵的右边界和下边界是大西洋，因此从矩阵的左边界和上边界开始反向搜索即可找到雨水流向太平洋的单元格，从矩阵的右边界和下边界开始反向搜索即可找到雨水流向大西洋的单元格。

可以使用深度优先搜索实现反向搜索，搜索过程中需要记录每个单元格是否可以从太平洋反向到达以及是否可以从大西洋反向到达。反向搜索结束之后，遍历每个网格，如果一个网格既可以从太平洋反向到达也可以从大西洋反向到达，则该网格满足太平洋和大西洋都可以到达，将该网格添加到答案中。

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


class Solution {
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        int m=heights.size(),n=heights[0].size();
        vector<vector<bool>> pacific(m,vector<bool>(n,false));
        vector<vector<bool>> atlantic(m,vector<bool>(n,false));
        for(int j=0;j<n;j++){
            dfs(heights,0,j,pacific);
            dfs(heights,m-1,j,atlantic);
        }
        for(int i=0;i<m;i++){
            dfs(heights,i,0,pacific);
            dfs(heights,i,n-1,atlantic);
        }
        vector<vector<int>> res;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(pacific[i][j] && atlantic[i][j]){
                    res.push_back({i,j});
                }
            }
        }
        return res;
    }
    void dfs(vector<vector<int>>& heights,int i,int j,vector<vector<bool>>& memo){
        if(memo[i][j]==true) return;
        int m=heights.size(),n=heights[0].size();
        memo[i][j]=true;
        vector<vector<int>> temp={{-1,0},{1,0},{0,-1},{0,1}};
        for(vector<int> t:temp){
            int row=i+t[0];
            int column=j+t[1];
            if(row>=0 && row<m && column>=0 && column<n && heights[row][column]>=heights[i][j]){
                dfs(heights,row,column,memo);
            }
        }
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45


class Solution {
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        int m=heights.size(),n=heights[0].size();
        vector<vector<bool>> pacific(m,vector<bool>(n,false));
        vector<vector<bool>> atlantic(m,vector<bool>(n,false));
        for(int j=0;j<n;j++){
            bfs(heights,0,j,pacific);
            bfs(heights,m-1,j,atlantic);
        }
        for(int i=0;i<m;i++){
            bfs(heights,i,0,pacific);
            bfs(heights,i,n-1,atlantic);
        }
        vector<vector<int>> res;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(pacific[i][j] && atlantic[i][j]){
                    res.push_back({i,j});
                }
            }
        }
        return res;
    }
    void bfs(vector<vector<int>>& heights,int i,int j,vector<vector<bool>>& memo){
        if(memo[i][j]==true) return;
        int m=heights.size(),n=heights[0].size();
        vector<vector<int>> temp={{-1,0},{1,0},{0,-1},{0,1}};
        queue<pair<int,int>> q;
        memo[i][j]=true;
        q.push({i,j});
        while(!q.empty()){
            auto [a,b]=q.front();
            q.pop();
            for(vector<int> t:temp){
                int row=a+t[0];
                int column=b+t[1];
                if(row>=0 && row<m && column>=0 && column<n && heights[row][column]>=heights[a][b] && !memo[row][column]){
                    memo[row][column]=true;
                    q.push({row,column});
                }
            }
        }
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

200 Number of Islands

DFS

在DFS的过程中，每个搜索到的 1 都会被重新标记为 0。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m=grid.size(),n=grid[0].size();
        int res=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]=='1'){
                    res+=1;
                    dfs(grid,i,j);
                }
            }
        }
        return res;
    }
    void dfs(vector<vector<char>>& grid,int row,int column){
        int m=grid.size(),n=grid[0].size();
        if(row>=0 && row<m && column>=0 && column<n && grid[row][column]=='1'){
            grid[row][column]='0';
            dfs(grid,row,column-1);
            dfs(grid,row-1,column);
            dfs(grid,row,column+1);
            dfs(grid,row+1,column);
        }
        return;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m=grid.size(),n=grid[0].size();
        int res=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]=='1'){
                    res+=1;
                    bfs(grid,i,j);
                }
            }
        }
        return res;
    }
    void bfs(vector<vector<char>>& grid,int i,int j){
        int m=grid.size(),n=grid[0].size();
        queue<pair<int,int>> q;
        q.push({i,j});
        while(!q.empty()){
            auto [row,column]=q.front();
            q.pop();
            if(row>=0 && row<m && column>=0 && column<n && grid[row][column]=='1'){
                grid[row][column]='0';
                q.push({row,column-1});
                q.push({row-1,column});
                q.push({row,column+1});
                q.push({row+1,column});
            }
        }
        return;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

886 Possible Bipartition

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
public:
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        vector<vector<int>> enemy(n+1);
        for(vector<int> dis:dislikes){
            enemy[dis[0]].push_back(dis[1]);
            enemy[dis[1]].push_back(dis[0]);
        }
        vector<int> color(n+1,0);
        //0：未分组 1：分组1 2:分组2
        //11(3)^01(1)=10(2) 11(3)^10(2)=01(1)
        for(int i=1;i<=n;i++){
            if(!color[i] && !dfs(enemy,color,i,1)){
                return false;
            }
        }
        return true;
    }
    bool dfs(vector<vector<int>>& enemy,vector<int>& color,int curNode,int newColor){
        color[curNode]=newColor;
        for(int nextNode:enemy[curNode]){
            //nextNode:0
            if(color[nextNode] && color[curNode]==color[nextNode]){
                return false;
            }
            //nextNode:已染色
            if(!color[nextNode] && !dfs(enemy,color,nextNode,3^newColor)){
                return false;
            }
        }
        return true;
    }
};

时间复杂度：O(n+m)
空间复杂度：O(n+m)

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
public:
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        vector<vector<int>> enemy(n+1);
        for(vector<int> dis:dislikes){
            enemy[dis[0]].push_back(dis[1]);
            enemy[dis[1]].push_back(dis[0]);
        }
        vector<int> color(n+1,0);
        //0：未分组 1：分组1 2:分组2
        //11(3)^01(1)=10(2) 11(3)^10(2)=01(1)
        for(int i=1;i<=n;i++){
            if(color[i]==0){
                queue<int> q;
                q.push(i);
                color[i]=1;
                while(!q.empty()){
                    int cur=q.front();
                    q.pop();
                    for(int next:enemy[cur]){
                        if(color[next]!=0 && color[cur]==color[next]){
                            return false;
                        } 
                        if(color[next]==0){
                            color[next]=3^color[cur];
                            q.push(next);
                        }
                    }
                }
            }
        }
        return true;
    }
};

时间复杂度：O(n+m)
空间复杂度：O(n+m)

Union Find

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


class Solution {
public:
    vector<int> father;
    bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
        vector<vector<int>> enemy(n+1);
        for(vector<int> dis:dislikes){
            enemy[dis[0]].push_back(dis[1]);
            enemy[dis[1]].push_back(dis[0]);
        }
        father.resize(n+1);
        for(int i=1;i<=n;i++){
            father[i]=i;
        }
        for(int i=1;i<=n;i++){
            for(int j=0;j<enemy[i].size();j++){
                Union(enemy[i][0],enemy[i][j]);
                if(isConnect(i,enemy[i][j])){
                    return false;
                }
            }
        }
        return true;
    }
    void Union(int a,int b){
        int fa=findFather(a);
        int fb=findFather(b);
        if(fa!=fb){
            father[fa]=fb;
        }
    }
    int findFather(int i){
        if(father[i]!=i){
            father[i]=findFather(father[i]);
        }
        return father[i];
    }
    bool isConnect(int a,int b){
        int fa=findFather(a);
        int fb=findFather(b);
        return fa==fb;
    }
};

时间复杂度：O(n+m)
空间复杂度：O(n+m)

934 Shortest Bridge

求最少的翻转 0 的数目等价于求矩阵中两个岛的最短距离，因此BFS来找到矩阵中两个块的最短距离。首先找到其中一座岛，然后将其不断向外延伸一圈，直到到达了另一座岛，延伸的圈数即为最短距离。BFS时，将已经遍历过的位置标记为 −1。

BFS

DFS

时间复杂度：O(n+m)
空间复杂度：O(n+m)

拓扑排序 Topological Sort

一种常用的拓扑排序算法是每次从有向无环图中取出一个入度为0的节点添加到拓扑排序序列之中，然后删除该节点及所有以它为起点的边。重复这个步骤，直到图为空或图中不存在入度为0的节点。如果最终图为空，那么图是有向无环图，此时就找到了该图的一个拓扑排序序列。如果最终图不为空并且已经不存在入度为0的节点，那么图中一定有环。

207 Course Schedule

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


class Solution {
public:
    vector<vector<int>> adjacent;
    vector<int> inDegree;
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        adjacent.resize(numCourses);
        inDegree.resize(numCourses);
        for(vector<int> pre:prerequisites){
            adjacent[pre[1]].push_back(pre[0]);
            inDegree[pre[0]]++;
        }
        queue<int> q;
        for(int i=0;i<numCourses;i++){
            if(inDegree[i]==0){
                q.push(i);
            }
        }
        int visit=0;
        while(!q.empty()){
            visit++;
            int cur=q.front();
            q.pop();
            for(int num:adjacent[cur]){
                inDegree[num]--;
                if(inDegree[num]==0){
                    q.push(num);
                }
            }
        }
        return visit==numCourses;
    }
};

时间复杂度：O(m+n)，节点的数目为m（变量numCourses），边的数目为n（数组prerequisites的长度）
空间复杂度：O(m+n)

DFS

通过 DFS 判断图中是否有环。

算法流程：借助一个标志列表 visit，用于判断每个节点 i （课程）的状态：

未被 DFS 访问：visit[i] == 0
已被其他节点启动的 DFS 访问：visit[i] == -1
已被当前节点启动的 DFS 访问：visit[i] == 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
public:
    vector<vector<int>> adjacency;
    vector<int> visit;
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        adjacency.resize(numCourses);
        visit.resize(numCourses);
        for(vector<int> pre:prerequisites){
            adjacency[pre[1]].push_back(pre[0]);
        }
        for(int i=0;i<numCourses;i++){
            if(!dfs(i)) return false;
        }
        return true;
    }
    bool dfs(int i){
        //已被其他节点启动的 DFS 访问
        if(visit[i]==-1) return true;
        //已被当前节点启动的 DFS 访问
        if(visit[i]==1) return false;
        visit[i]=1;
        for(int j:adjacency[i]){
            if(!dfs(j)) return false;
        }
        visit[i]=-1;
        return true;
    }
};

时间复杂度：O(m+n)，节点的数目为m（变量numCourses），边的数目为n（数组prerequisites的长度）
空间复杂度：O(m+n)

210 Course Schedule II

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> adjacency(numCourses);
        vector<int> inDegree(numCourses);
        for(vector<int> pre:prerequisites){
            adjacency[pre[1]].push_back(pre[0]);
            inDegree[pre[0]]++;
        }
        vector<int> order;
        queue<int> q;
        for(int i=0;i<numCourses;i++){
            if(inDegree[i]==0){
                q.push(i);
            }
        }
        while(!q.empty()){
            int cur=q.front();
            q.pop();
            order.push_back(cur);
            for(int next:adjacency[cur]){
                inDegree[next]--;
                if(inDegree[next]==0){
                    q.push(next);
                }
            }
        }
        if(order.size()!=numCourses) return {};
        return order;
    }
};

注意：

1、拓扑排序返回结果order不能初始化为numCourses大小，否则出错（排查了挺久的错误🫠）。

2、If it is impossible to finish all courses, return an empty array.

注意有环时，order的大小不等于numCourses，所以返回{}。

时间复杂度：O(m+n)，节点的数目为m（变量numCourses），边的数目为n（数组prerequisites的长度）
空间复杂度：O(m+n)

剑指 Offer II 114. 外星文字典

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


class Solution {
public:
    string alienOrder(vector<string>& words) {
        unordered_map<char,unordered_set<char>> adjacency;
        unordered_map<char,int> inDegree;
        for(string word:words){
            for(char ch:word){
                adjacency[ch]=unordered_set<char>();
                inDegree[ch]=0;
            }
        }
        for(int i=1;i<words.size();i++){
            string a=words[i-1];
            string b=words[i];
            //abc ab
            if(a.substr(0,b.length())==b && a!=b){
                return "";
            }
            for(int j=0;j<a.length() && j<b.length();j++){
                if(a[j]!=b[j]){
                    if(!adjacency[a[j]].count(b[j])){
                        adjacency[a[j]].insert(b[j]);
                        inDegree[b[j]]++;
                    }
                    break;
                }
            }
        }
        queue<char> q;
        for(auto it=adjacency.begin();it!=adjacency.end();it++){
            char ch=it->first;
            if(inDegree[ch]==0){
                q.push(ch);
            }
        }
        string order;
        while(!q.empty()){
            char cur=q.front();
            q.pop();
            order+=cur;
            for(auto& ch:adjacency[cur]){
                inDegree[ch]--;
                if(inDegree[ch]==0){
                    q.push(ch);
                }
            }
        }
        return order.length()==adjacency.size()?order:"";
    }
};

这里有一类特殊的输入需要特别注意。如果排在后面的单词是排在前面的单词的前缀，那么无论什么样的字母顺序都是不可能的。例如，如果排序的单词列表是[“abc”，“ab”]，不管是什么样的字母顺序，“abc"都不可能排在"ab"的前面，因此这是一个无效的输入，此时可以直接返回空字符串表示无效的字母顺序。

如果单词列表的长度为m，平均每个单词的长度为n，由于上述代码在构建有向图时需要扫描并比较每个字母，因此构建有向图的时间复杂度是O（mn）。该外星文的所有字母为英文字母。有向图中的节点为外星文的字母，最多只有26个，可以将其看成常数。最多根据单词列表words相邻的两个单词在图中添加一条边，所以边的数目是O（n）。于是，采用广度优先搜索的拓扑排序的时间复杂度是O（n）。综合来看，上述算法的总的时间复杂度是O（mn）。

时间复杂度：O(mn)
空间复杂度：O(m+n)

剑指 Offer II 115. 重建序列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


class Solution {
public:
    bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) {
        unordered_map<int,unordered_set<int>> adjacency;
        unordered_map<int,int> inDegree;
        vector<int> res;
        for(int i=1;i<=nums.size();i++){
            adjacency[i]=unordered_set<int>();
            inDegree[i]=0;
        }
        for(vector<int> seq:sequences){
            for(int i=1;i<seq.size();i++){
                if(!adjacency[seq[i-1]].count(seq[i])){
                    adjacency[seq[i-1]].insert(seq[i]);
                    inDegree[seq[i]]++;
                }
            }
        }
        queue<int> q;
        for(auto it=inDegree.begin();it!=inDegree.end();it++){
            if(it->second==0){
                q.push(it->first);
            }
        }
        while(q.size()==1){
            int cur=q.front();
            q.pop();
            res.push_back(cur);
            for(int next:adjacency[cur]){
                inDegree[next]--;
                if(inDegree[next]==0){
                    q.push(next);
                }
            }
        }
        if(res==nums) return true;
        return false;
    }
};

注意：

1、adjacency 和 inDegree 的初始化不可缺少。

for(int i=1;i<=nums.size();i++){ adjacency[i]=unordered_set(); inDegree[i]=0; }

2、这里map的value使用的是unordered_set<int>，并且构造图的adjacency邻接表的时候需要检查是否已经加入这条边，否则inDegree会多次增加，导致算法错误。

if(!adjacency[seq[i-1]].count(seq[i])){ adjacency[seq[i-1]].insert(seq[i]); inDegree[seq[i]]++; }

例如：nums=[4,1,5,2,6,3], sequences= [[5,2,6,3],[4,1,5,2]]

如果图中节点的数目为v（nums.size）、边的数目为e（O（∑sequences[i].size）），那么构建有向图和基于广度优先搜索进行拓扑排序的时间复杂度都是O（v+e），因此总体时间复杂度是O（v+e）。

时间复杂度：O(v+e)
空间复杂度：O(v+e)

并查集 Union Find

547 Number of Provinces

输入的矩阵isConnected是沿着对角线对称的。矩阵isConnected对角线上的所有数字都是1。

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int cities=isConnected.size();
        vector<bool> visited(cities,false);
        int provinces=0;
        queue<int> q;
        for(int i=0;i<cities;i++){
            if(!visited[i]){
                q.push(i);
                while(!q.empty()){
                    int cur=q.front();
                    q.pop();
                    visited[cur]=true;
                    for(int j=0;j<cities;j++){
                        if(isConnected[cur][j]==1 && !visited[j]){
                            q.push(j);
                        }
                    }
                }
                provinces++;
            }
        }
        return provinces;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(n)

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int cities=isConnected.size();
        vector<bool> visited(cities,false);
        int provinces=0;
        for(int i=0;i<cities;i++){
            if(!visited[i]){
                dfs(isConnected,visited,cities,i);
                provinces++;
            }
        }
        return provinces;
    }
    void dfs(vector<vector<int>>& isConnected,vector<bool>& visited,int cities,int i){
        for(int j=0;j<cities;j++){
            if(isConnected[i][j]==1 && !visited[j]){
                visited[j]=true;
                dfs(isConnected,visited,cities,j);
            }
        }
    }
};

时间复杂度：O(n^2)
空间复杂度：O(n)

Union Find

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int cities=isConnected.size();
        vector<int> father(cities);
        for(int i=0;i<cities;i++){
            father[i]=i;
        }
        int provinces=cities;
        for(int i=0;i<cities;i++){
            for(int j=i+1;j<cities;j++){
                if(isConnected[i][j]==1 && Union(father,i,j)){
                    provinces--;
                }
            }
        }
        return provinces;
    }
    int findFather(vector<int>& father,int i){
        if(father[i]!=i){
            father[i]=findFather(father,father[i]);
        }
        return father[i];
    }
    bool Union(vector<int>& father,int i,int j){
        int fa=findFather(father,i);
        int fb=findFather(father,j);
        if(fa!=fb){
            father[fa]=fb;
            return true;
        }
        return false;
    }
};

n 是城市的数量。需要遍历矩阵 isConnected 中的所有元素，时间复杂度是 O(n^2)，如果遇到相连关系，则需要进行 2 次查找和最多 1次合并，一共需要进行 2n^2 次查找和最多 n^2 次合并，因此总时间复杂度是 O(2n^2logn)=O(n^2logn)。这里的并查集使用了路径压缩，但是没有使用按秩合并，最坏情况下的时间复杂度是 O(n^2logn)，平均情况下的时间复杂度依然是 O(n^2*α(n))，其中 α 为阿克曼函数的反函数，α(n) 可以认为是一个很小的常数，α（n）在n十分大时还是小于5。

时间复杂度：O(n^2logn)
空间复杂度：O(n)

findFather的迭代写法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


	int findFather(vector<int>& father,int i){
        int a=i;
        while(father[i]!=i){
            i=father[i];
        }
        while(father[a]!=a){
            int b=a;
            a=father[a];
            father[b]=i;
        }
        return i;
    }

839 Similar String Groups

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


class Solution {
public:
    vector<int> father;
    bool check(string s,string t){
        int len=s.length();
        int diffNum=0;
        for(int i=0;i<len;i++){
            if(s[i]!=t[i]){
                diffNum++;
                if(diffNum>2) return false;
            }
        }
        return true;
    }
    int findFather(int i){
        if(father[i]!=i){
            father[i]=findFather(father[i]);
        }
        return father[i];
    }
    int numSimilarGroups(vector<string>& strs) {
        int n=strs.size();
        father.resize(n);
        for(int i=0;i<n;i++){
            father[i]=i;
        }
        for(int i=0;i<n;i++){
            for(int j=i+1;j<n;j++){
                int fa=findFather(i);
                int fb=findFather(j);
                if(fa==fb){
                    continue;
                }
                if(check(strs[i],strs[j])){
                    father[fa]=fb;
                }
            }
        }
        int res=0;
        for(int i=0;i<n;i++){
            if(father[i]==i){
                res++;
            }
        }
        return res;
    }
};

时间复杂度：O(n^2m+nlogn)。n 是字符串的数量。需要 O(n^2) 地枚举任意一对字符串之间的关系，对于任意一对字符串，需要 O(m) 的时间检查字符串是否相同。在最坏情况下我们需要对并查集执行 O(n) 次合并，合并的均摊时间复杂度 O(log n)。综上，总的时间复杂度为 O(n^2m+nlogn)。
空间复杂度：O(n)

684 Redundant Connection

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
public:
    vector<int> father;
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n=edges.size();
        father.resize(n+1);
        for(int i=1;i<=n;i++){
            father[i]=i;
        }
        for(vector<int> edge:edges){
            int i=edge[0],j=edge[1];
            int fa=findFather(i);
            int fb=findFather(j);
            if(fa!=fb){
                father[fa]=fb;
            }else{
                return {i,j};
            }
        }
        return {};
    }
    int findFather(int i){
        if(father[i]!=i){
            father[i]=findFather(father[i]);
        }
        return father[i];
    }
};

时间复杂度：O(nlogn)
空间复杂度：O(n)

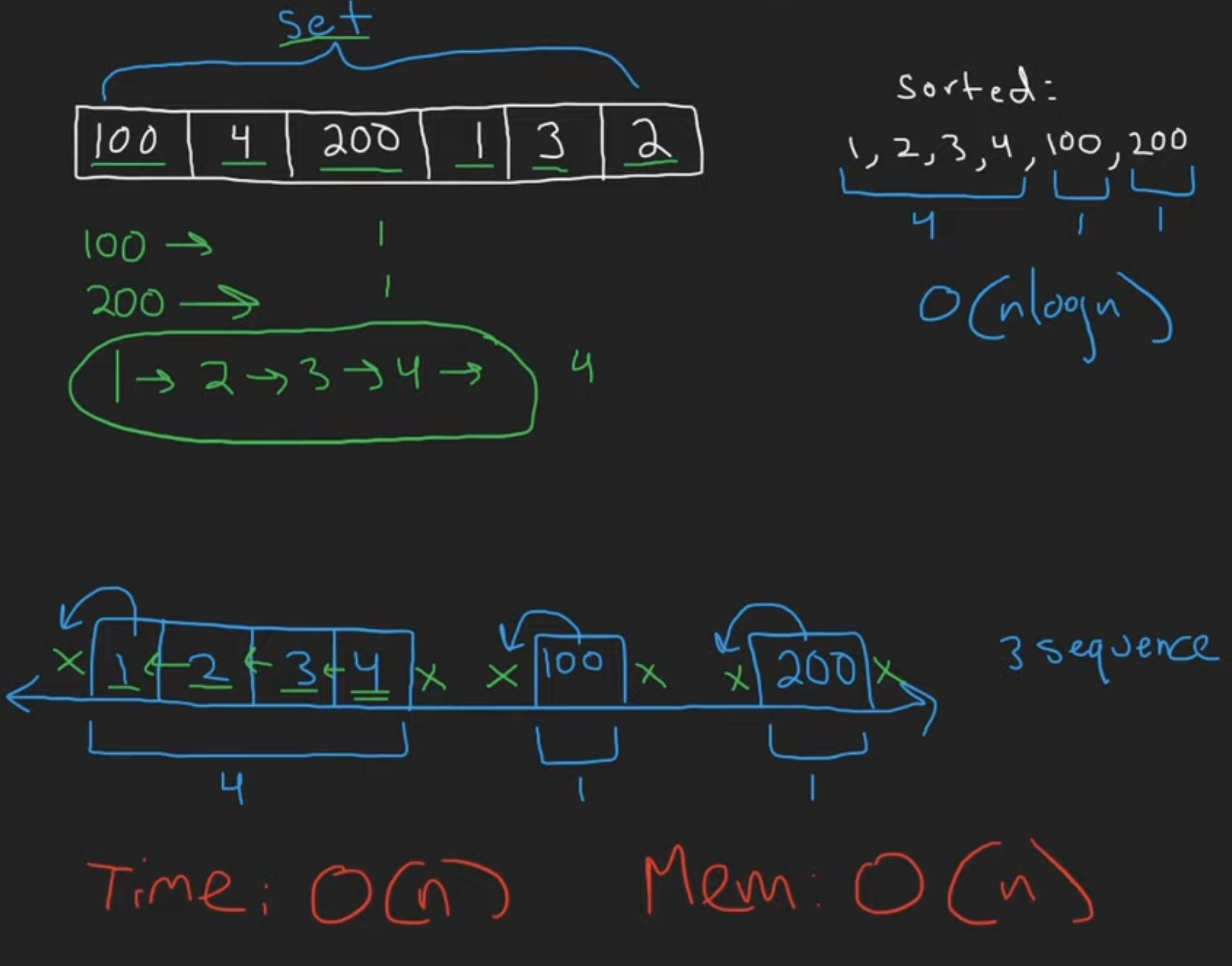
128 Longest Consecutive Sequence

Hash Table

128-set

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> s;
        for(int num:nums){
            s.insert(num);
        }
        int longest=0;
        for(int num:s){
            if(!s.count(num-1)){
                int cur=num;
                int length=1;
                while(s.count(cur+1)){
                    cur+=1;
                    length+=1;
                }
                longest=max(longest,length);
            }
        }
        return longest;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

Union Find

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


class Solution {
public:
    unordered_map<int,int> father;
    unordered_map<int,int> count;
    int longestConsecutive(vector<int>& nums) {
        int n=nums.size();
        unordered_set<int> s;
        for(int i=0;i<n;i++){
            int num=nums[i];
            s.insert(num);
            father[num]=num;
            count[num]=1;
        }
        for(auto num:s){
            if(s.count(num-1)){
                Union(num,num-1);
            }
            if(s.count(num+1)){
                Union(num,num+1);
            }
        }
        int longest=0;
        for(auto it=count.begin();it!=count.end();it++){
            longest=max(count[it->first],longest);
        }
        return longest;
    }
    int findFather(int i){
        if(father[i]!=i){
            father[i]=findFather(father[i]);
        }
        return father[i];
    }
    void Union(int i,int j){
        int fa=findFather(i);
        int fb=findFather(j);
        if(fa!=fb){
            father[fa]=fb;
            count[father[fa]]=count[fa]+count[fb];
        }
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


class Solution {
public:
    unordered_set<int> s;
    int longestConsecutive(vector<int>& nums) {
        int n=nums.size();
        for(int num:nums){
            s.insert(num);
        }
        int longest=0;
        while(!s.empty()){
            auto it=s.begin();
            longest=max(longest,bfs(*it));
        }
        return longest;
    }
    int bfs(int num){
        queue<int> q;
        q.push(num);
        s.erase(num);
        int length=1;
        while(!q.empty()){
            int cur=q.front();
            q.pop();
            if(s.count(cur-1)){
                q.push(cur-1);
                s.erase(cur-1);
                length++;
            }
            if(s.count(cur+1)){
                q.push(cur+1);
                s.erase(cur+1);
                length++;
            }
        }
        return length;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

Matrix

73 Set Matrix Zeroes

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size(),n=matrix[0].size();
        unordered_set<int> row;
        unordered_set<int> column;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(matrix[i][j]==0){
                    row.insert(i);
                    column.insert(j);
                }
            }
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(row.count(i) || column.count(j)) matrix[i][j]=0;
            }
        }
    }
};

时间复杂度：O(mn)
空间复杂度：O(m+n)

a constant space solution:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size(),n=matrix[0].size();
        bool flagrow=false,flagcolumn=false;
        for(int i=0;i<m;i++){
            if(!matrix[i][0]){
                flagcolumn=true;
            }
        }
        for(int j=0;j<n;j++){
            if(!matrix[0][j]){
                flagrow=true;
            }
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(!matrix[i][j]){
                    matrix[i][0]=matrix[0][j]=0;
                }
            }
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(!matrix[i][0] || !matrix[0][j]){
                    matrix[i][j]=0;
                }
            }
        }
        if(flagcolumn){
            for(int i=0;i<m;i++){
                matrix[i][0]=0;
            }
        }
        if(flagrow){
            for(int j=0;j<n;j++){
                matrix[0][j]=0;
            }
        }
    }
};

时间复杂度：O(mn)
空间复杂度：O(1)

54 Spiral Matrix

首先设定上下左右边界
其次向右移动到最右，此时第一行因为已经使用过了，可以将其从图中删去，体现在代码中就是重新定义上边界
判断若重新定义后，上下边界交错，表明螺旋矩阵遍历结束，跳出循环，返回答案
若上下边界不交错，则遍历还未结束，接着向下向左向上移动，操作过程与第一，二步同理
不断循环以上步骤，直到某两条边界交错，跳出循环，返回答案。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;
        if(matrix.empty()) return res;
        int up=0,down=matrix.size()-1;
        int left=0,right=matrix[0].size()-1;
        while(true){
            for(int i=left;i<=right;i++) res.push_back(matrix[up][i]);
            if(++up>down) break;
            for(int i=up;i<=down;i++) res.push_back(matrix[i][right]);
            if(--right<left) break;
            for(int i=right;i>=left;i--) res.push_back(matrix[down][i]);
            if(--down<up) break;
            for(int i=down;i>=up;i--) res.push_back(matrix[i][left]);
            if(++left>right) break;
        }
        return res;
    }
};

时间复杂度：O(mn)
空间复杂度：O(1)

48 Rotate Image

辅助数组

矩阵旋转后，对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        // C++ 这里的 = 拷贝是值拷贝，会得到一个新的数组
        auto new_matrix=matrix;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                //matrix[row][column] --> new_matrix[column][n-row-1];
                new_matrix[j][n-i-1]=matrix[i][j];
            }
        }
        matrix=new_matrix;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(n^2)

翻转

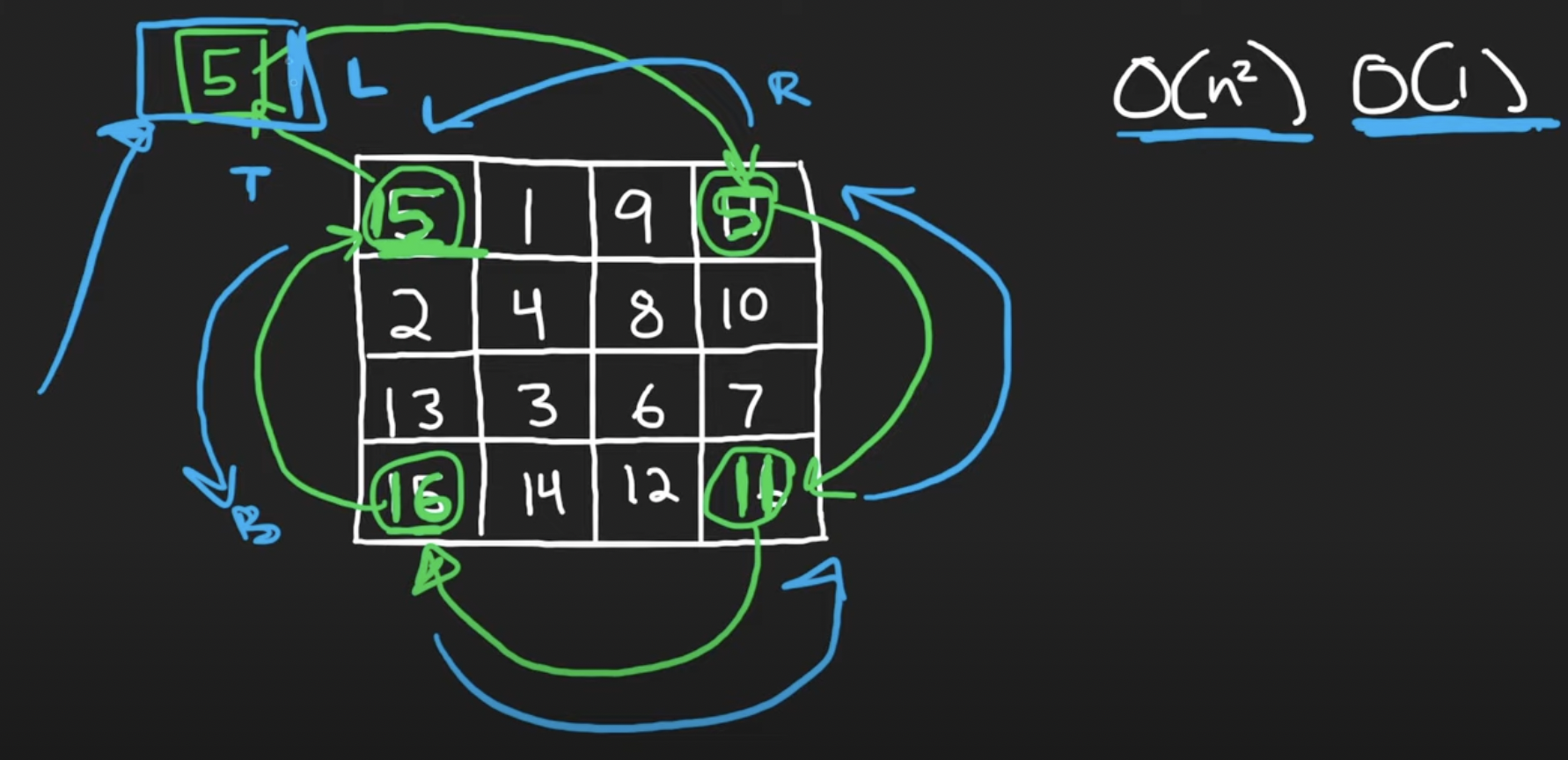
leetcode-48

rotate image in-place:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        int left=0,right=n-1;
        while(left<right){
            int top=left,bottom=right;
            for(int i=0;i<right-left;i++){
                int topleft=matrix[top][left+i];
                matrix[top][left+i]=matrix[bottom-i][left];
                matrix[bottom-i][left]=matrix[bottom][right-i];
                matrix[bottom][right-i]=matrix[top+i][right];
                matrix[top+i][right]=topleft;
            }
            left++;
            right--;
        }
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

利用矩阵旋转来翻转

rotate image in-place:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        // 水平翻转
        for(int i=0;i<n/2;i++){
            for(int j=0;j<n;j++){
                swap(matrix[i][j],matrix[n-i-1][j]);
            }
        }
        // 对角线翻转
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                swap(matrix[i][j],matrix[j][i]);
            }
        }
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

79 Word Search

Backtrack

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int m=board.size(),n=board[0].size();
        vector<vector<bool>> visited(m,vector<bool>(n,false));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(board[i][j]!=word[0]) continue;
                if(backtrack(board,visited,i,j,word,0)){
                    return true;
                }
            }
        }
        return false;
    }
    bool backtrack(vector<vector<char>>& board,vector<vector<bool>>& visited,int i,int j,string word,int index){
        int m=board.size(),n=board[0].size();
        if(i<0 || i==m || j<0 || j==n || board[i][j]!=word[index] || visited[i][j]) return false;
        if(board[i][j]==word[index] && index==word.length()-1) return true;
        visited[i][j]=true;
        if(backtrack(board,visited,i,j-1,word,index+1) ||
          backtrack(board,visited,i-1,j,word,index+1) ||
          backtrack(board,visited,i,j+1,word,index+1) ||
          backtrack(board,visited,i+1,j,word,index+1)) return true;
        visited[i][j]=false;
        return false;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


class Solution {
public:
    vector<vector<bool>> visited;
    bool exist(vector<vector<char>>& board, string word) {
        int m=board.size(),n=board[0].size();
        visited.resize(m,vector<bool>(n,false));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(board[i][j]!=word[0]) continue;
                if(backtrack(board,i,j,word,0)){
                    return true;
                }
            }
        }
        return false;
    }
    bool backtrack(vector<vector<char>>& board,int i,int j,string word,int index){
        int m=board.size(),n=board[0].size();
        if(i<0 || i==m || j<0 || j==n || board[i][j]!=word[index] || visited[i][j]) return false;
        if(board[i][j]==word[index] && index==word.length()-1) return true;
        visited[i][j]=true;
        if(backtrack(board,i,j-1,word,index+1) ||
          backtrack(board,i-1,j,word,index+1) ||
          backtrack(board,i,j+1,word,index+1) ||
          backtrack(board,i+1,j,word,index+1)) return true;
        visited[i][j]=false;
        return false;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

DFS

为了防止重复遍历相同的位置，需要额外维护一个与 board 等大的 visited 数组，用于标识每个位置是否被访问过。每次遍历相邻位置时，需要跳过已经被访问的位置。

官方解（自己写的一直TLE😭）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


class Solution {
public:
    bool check(vector<vector<char>>& board, vector<vector<int>>& visited, int i, int j, string& s, int k) {
        if (board[i][j] != s[k]) {
            return false;
        } else if (k == s.length() - 1) {
            return true;
        }
        visited[i][j] = true;
        vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        bool result = false;
        for (const auto& dir: directions) {
            int newi = i + dir.first, newj = j + dir.second;
            if (newi >= 0 && newi < board.size() && newj >= 0 && newj < board[0].size()) {
                if (!visited[newi][newj]) {
                    bool flag = check(board, visited, newi, newj, s, k + 1);
                    if (flag) {
                        result = true;
                        break;
                    }
                }
            }
        }
        visited[i][j] = false;
        return result;
    }

    bool exist(vector<vector<char>>& board, string word) {
        int h = board.size(), w = board[0].size();
        vector<vector<int>> visited(h, vector<int>(w));
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                bool flag = check(board, visited, i, j, word, 0);
                if (flag) {
                    return true;
                }
            }
        }
        return false;
    }
};

时间复杂度：O(mn)
空间复杂度：O(mn)

36 Valid Sudoku

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        unordered_map<int,unordered_set<int>> row,column,box;
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                char ch=board[i][j];
                if(ch=='.') continue;
                int num=ch-'0';
                int id=j/3+(i/3)*3;
                if(row[i].count(num) || column[j].count(num) || box[id].count(num)) return false;
                row[i].insert(num);
                column[j].insert(num);
                box[id].insert(num);
            }
        }
        return true;
    }
};

时间复杂度：O(1)
空间复杂度：O(1)

大多数的哈希表计数问题，都能转换为使用数组解决。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        vector<vector<int>> row(9,vector<int>(10,0)),column(9,vector<int>(10,0)),box(9,vector<int>(10,0));
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                char ch=board[i][j];
                if(ch=='.') continue;
                int num=ch-'0';
                int id=j/3+(i/3)*3;
                if(row[i][num]==1 || column[j][num]==1 || box[id][num]==1) return false;
                row[i][num]=1;
                column[j][num]=1;
                box[id][num]=1;
            }
        }
        return true;
    }
};

时间复杂度：O(1)
空间复杂度：O(1)

Table of Contents

图

图的搜索

695 Max Area of Island

DFS(Recursive)

DFS(Stack)

BFS

785 Is Graph Bipartite?

DFS

BFS

542 01 Matrix

BFS

752 Open the Lock

797 All Paths From Source to Target

399 Evaluate Division

329 Longest Increasing Path in a Matrix

记忆化DFS

417 Pacific Atlantic Water Flow

200 Number of Islands

DFS

BFS

886 Possible Bipartition

DFS

BFS

Union Find

934 Shortest Bridge

BFS

DFS

拓扑排序 Topological Sort

207 Course Schedule

BFS

DFS

210 Course Schedule II

剑指 Offer II 114. 外星文字典

BFS

剑指 Offer II 115. 重建序列

并查集 Union Find

547 Number of Provinces

BFS

DFS

Union Find

839 Similar String Groups

684 Redundant Connection

128 Longest Consecutive Sequence

Hash Table

Union Find

BFS

Matrix

73 Set Matrix Zeroes

54 Spiral Matrix

48 Rotate Image

辅助数组

翻转

利用矩阵旋转来翻转

79 Word Search

Backtrack

DFS

36 Valid Sudoku