LeetCode + 《剑指Offer II》刷题笔记。
整数
001. 整数除法
剑指 Offer II 001. 整数除法
由于是整数除法并且除数不等于0,因此商的绝对值一定<=被除数的绝对值。因此,int型整数的除法只有一种情况会导致溢出,即:-2^31/-1=2^31,超出int的最大值2^31-1,故返回INT_MAX。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Solution {
public:
int divide(int dividend, int divisor) {
//特殊情况:-2^31/-1=2^31 超出int的最大值2^31-1,故返回INT_MAX
if(dividend==0x80000000 && divisor==-1){
return INT_MAX;
}
//这边negative的设计真的很巧妙
int negative=2;
if(dividend>0){
negative--;
dividend=-dividend;
}
if(divisor>0){
negative--;
divisor=-divisor;
}
int result=divideCore(dividend,divisor);
return negative==1?-result:result;
}
int divideCore(int dividend,int divisor){
int result=0;
//dividend和divisor都已经是负数,所以是dividend<=divisor
while(dividend<=divisor){
int quotient=1;
int value=divisor;
while(value>=0xc0000000 && dividend<=value+value){
quotient+=quotient;
value+=value;
}
result+=quotient;
dividend-=value;
}
return result;
}
};
|
作者是用Java写的,而这份答案使用C++改写提交会出现“执行出错”的错误:
1
2
|
Line 28: Char 25: runtime error: signed integer overflow: 1073741824 + 1073741824 cannot be represented in type 'int' (solution.cpp)
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:37:25
|
正好LeetCode给出了:
1
2
3
|
最后执行的输入:
-2147483648
1
|
因此只要在原答案中加入:
1
2
3
|
if(dividend==0x80000000 && divisor==1){
return dividend;
}
|
就可运行通过。
后来又试了下Java,发现只要有-2^31/-1=2^31这一个特例就行。不知道这边C++和Java到底是什么原因导致的差别。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public int divide(int dividend, int divisor) {
if(dividend==0x80000000 && divisor==-1){
return Integer.MAX_VALUE;
}
int negative=2;
if(dividend>0){
negative--;
dividend=-dividend;
}
if(divisor>0){
negative--;
divisor=-divisor;
}
int result=divideCore(dividend,divisor);
return negative==1?-result:result;
}
private int divideCore(int dividend,int divisor){
int result=0;
while(dividend<=divisor){
int quotient=1;
int value=divisor;
while(value>=0xc0000000 && dividend<=value+value){
quotient+=quotient;
value+=value;
}
result+=quotient;
dividend-=value;
}
return result;
}
}
|
官方题:29. 两数相除
官方解答案的特例太多了,《剑指Offer II》作者编写的代码的确是巧妙精简。
002. 二进制加法
剑指 Offer II 002. 二进制加法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
string addBinary(string a, string b) {
//模拟二进制加法,逢二进一
string result;
int i=a.length()-1;
int j=b.length()-1;
int carry=0;
while(i>=0 || j>=0){
int digitA= i>=0?(a[i--]-'0'):0;
int digitB= j>=0?(b[j--]-'0'):0;
int sum=digitA+digitB+carry;
carry=0;
if(sum>=2){
carry=1;
sum-=2;
}
result+=char(sum+'0');
}
if(carry==1) result+='1';
reverse(result.begin(),result.end());
return result;
}
};
|
这里的一步极其重要,即判断通过判断下标赋予digitA、digitB本身的值或0,可以在一个循环内完成长度不同的字符串相加,而不用将两个字符串修正为长度相同。
1
2
3
4
5
|
while(i>=0 || j>=0){
int digitA= i>=0?(a[i--]-'0'):0;
int digitB= j>=0?(b[j--]-'0'):0;
...
}
|
将a、b两个字符串修正为长度相同:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
string addBinary(string a, string b) {
int lena=a.length();
int lenb=b.length();
int len;
if(lena>lenb){
b.insert(0,lena-lenb,'0');
len=lena;
}else{
a.insert(0,lenb-lena,'0');
len=lenb;
}
int carry=0;
string result;
for(int i=len-1;i>=0;i--){
int sum=a[i]-'0'+b[i]-'0'+carry;
result+=(sum%2+'0');
carry=sum/2;
}
if(carry>0){
result+='1';
}
reverse(result.begin(),result.end());
return result;
}
};
|
Java(作者的解法):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public String addBinary(String a, String b) {
StringBuilder result=new StringBuilder();
int i=a.length()-1;
int j=b.length()-1;
int carry=0;
while(i>=0 || j>=0){
int digitA= i>=0?a.charAt(i--)-'0':0;
int digitB= j>=0?b.charAt(j--)-'0':0;
int sum=digitA+digitB+carry;
carry= sum>=2 ? 1:0;
sum= sum>=2 ? sum-2:sum;
result.append(sum);
}
if(carry==1){
result.append(1);
}
return result.reverse().toString();
}
}
|
在Java中,int型数值可以直接append到StringBuilder上。
官方题: 67. 二进制求和
003. 前 n 个数字二进制中 1 的个数
剑指 Offer II 003. 前 n 个数字二进制中 1 的个数
问题:求一个整数i的二进制形式中1的个数
利用 i & (i−1) 简单计算
对于任意整数 i,令 i = i & (i−1),该运算将 i 的二进制表示的最后一个 1 变成 0。因此,对 i重复该操作,直到 i 变成 0,操作次数即为 i 的「一比特数」。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
int countOnes(int n){
int count=0;
while(n){
n &= (n-1);
count++;
}
return count;
}
vector<int> countBits(int n) {
vector<int> result(n+1);
for(int i=1;i<=n;i++){
result[i]=countOnes(i);
}
return result;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int[] countBits(int n) {
int[] result=new int[n+1];
for(int i=1;i<=n;i++){
int temp=i;
while(temp!=0){
temp &= (temp-1);
result[i]++;
}
}
return result;
}
}
|
时间复杂度:对于给定的 n,计算从 0 到 n的每个整数的「一比特数」的时间都不会超过 O(log n),因此总时间复杂度为 O(nlogn)。
空间复杂度:O(1)
利用 i & (i−1) 动态规划
整数i的二进制形式中1的个数比“i&(i-1)”的二进制形式中1的个数多1。可以利用这个规律。
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
vector<int> countBits(int n) {
vector<int> result(n+1);
for(int i=1;i<=n;i++){
result[i]=result[i & (i-1)]+1;
}
return result;
}
};
|
时间复杂度:O(n)。对于每个整数,只需要 O(1) 的时间计算「一比特数」。
空间复杂度:O(1)
利用 i/2 动态规划
如果正整数i是一个偶数,那么i相当于将“i/2”左移一位的结果,因此偶数i和“i/2”的二进制形式中1的个数是相同的。如果i是奇数,那么i相当于将“i/2”左移一位之后再将最右边一位设为1的结果,因此奇数i的二进制形式中1的个数比“i/2”的1的个数多1。
例如,整数3的二进制形式是11,有2个1。偶数6的二进制形式是110,有2个1。奇数7的二进制形式是111,有3个1。我们可以根据3的二进制形式中1的个数直接求出6和7的二进制形式中1的个数。
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
vector<int> countBits(int n) {
vector<int> result(n+1);
for(int i=1;i<=n;i++){
result[i]= result[i >> 1] + (i & 1);
}
return result;
}
};
|
用“i»1”计算“i/2”,用“i&1”计算“i%2”,位运算比除法运算和求余运算更高效。
时间复杂度:O(n)
空间复杂度:O(1)
官方题:338. 比特位计数
004. 只出现一次的数字
剑指 Offer II 004. 只出现一次的数字
使用辅助空间unordered_map(哈希表)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
int n=nums.size();
unordered_map<int,int> mp;
for(int i=0;i<n;i++){
mp[nums[i]]++;
}
for(int i=0;i<n;i++){
if(mp[nums[i]]==1) return nums[i];
}
return -1;
}
};
|
使用辅助空间Set(数学方法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
set<int> s;
long sumNum=0;
long sumSet=0;
for(int num:nums){
sumNum+=num;
if(s.find(num)!=s.end()) continue;
s.insert(num);
sumSet+=num;
}
return (3*sumSet-sumNum)/2;
}
};
|
使用位运算
简化版的类似的题目“输入数组中除一个数字只出现一次之外其他数字都出现两次,请找出只出现一次的数字”。
解法:任何一个数字异或它自己的结果都是0。如果将数组中所有数字进行异或运算,那么最终的结果就是那个只出现一次的数字。
一个整数是由32个0或1组成的。我们可以将数组中所有数字的同一位置的数位相加。如果将出现3次的数字单独拿出来,那么这些出现了3次的数字的任意第i个数位之和都能被3整除。
因此,如果数组中所有数字的第i个数位相加之和能被3整除,那么只出现一次的数字的第i个数位一定是0;如果数组中所有数字的第i个数位相加之和被3除余1,那么只出现一次的数字的第i个数位一定是1。这样只出现一次的任意第i个数位可以由数组中所有数字的第i个数位之和推算出来。当我们知道一个整数任意一位是0还是1之后,就可以知道它的数值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public int singleNumber(int[] nums) {
//bitSums[i]:保存数组nums中所有整数的二进制形式中第i个数位之和。
int[] bitSums=new int[32];
for(int num:nums){
for(int i=0;i<32;i++){
//( num >> (31-i) )&1:整数num的二进制形式中从左数起第i个数位。
bitSums[i] += (num >> (31-i)) & 1;
}
}
int result=0;
for(int i=0;i<32;i++){
result=(result<<1)+bitSums[i]%3;
}
return result;
}
}
|
(num >> (31-i)) & 1:整数num的二进制形式中从左数起第i个数位。
- 整数i先被
右移31-i位,原来从左数起第i个数位右移之后位于最右边。
- 与1做位与&运算:整数1除了最右边一位是1,其余数位都是0,它与任何一个数字做位与运算的结果都是保留数字的最右边一位,其他数位都被清零。
- 如果整数num从左数起第i个数位是1,那么“(num»(31-i))&1”的最终结果就是1;否则最终结果为0。
下面求8位二进制整数01101100从左数起的第2个(从0开始计数)数位。我们先将01101100右移5位(7-2=5)得到00000011,再将它和00000001做位与运算,结果为00000001,即1。8位二进制整数01101100从左边数起的第2个数位的确是1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
vector<int> bits(32,0);
for(int num:nums){
for(int i=0;i<32;i++){
bits[i] += (num>>i)&1;
}
}
int result=0;
for(int i=0;i<32;i++){
result += (bits[i]%3)<<i;
}
return result;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
vector<int> bits(32,0);
int result=0;
for(int i=0;i<32;i++){
for(int num:nums){
bits[i] += (num>>i)&1;
}
result |= (bits[i]%3)<<i;
}
return result;
}
};
|
005. 单词长度的最大乘积
剑指 Offer II 005. 单词长度的最大乘积
哈希表
普通做法:遍历字符串数组words 中的每一对单词,判断这一对单词是否有公共字母,如果没有公共字母,则用这一对单词的长度乘积更新最大单词长度乘积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public int maxProduct(String[] words) {
boolean[][] flags=new boolean[words.length][26];
for(int i=0;i<words.length;i++){
for(char c:words[i].toCharArray()){
flags[i][c-'a']=true;
}
}
int result=0;
for(int i=0;i<words.length;i++){
for(int j=i+1;j<words.length;j++){
int k=0;
for(;k<26;k++){
if(flags[i][k] && flags[j][k]){
break;
}
}
if(k==26){
int prod=words[i].length()*words[j].length();
result=Math.max(result,prod);
}
}
}
return result;
}
}
|
时间复杂度:O(nk+n^2)(如果数组words的长度为n,平均每个字符串的长度为k)
空间复杂度:O(n)
位运算:整数的二进制位
Java中int型整数的二进制形式有32位,但只需要26位就能表示一个字符串中出现的字符,因此可以用一个int型整数记录某个字符串中出现的字符。如果字符串中包含’a’,那么整数最右边的数位为1;如果字符串中包含’b’,那么整数的倒数第2位为1,其余以此类推。
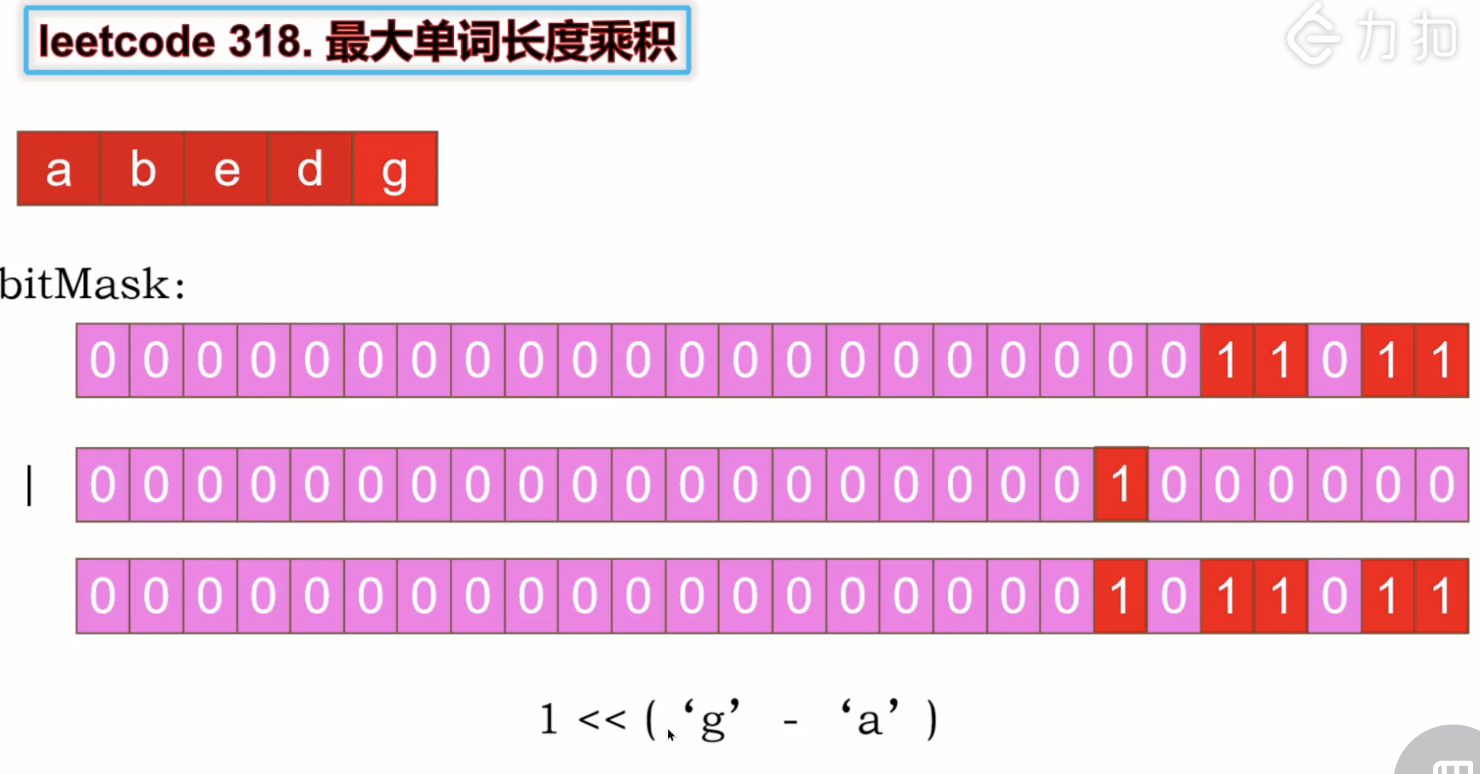
这样做的好处是能更快地判断两个字符串是否包含相同的字符。如果两个字符串中包含相同的字符,那么它们对应的整数相同的某个数位都为1,两个整数的与运算将不会等于0。如果两个字符串没有相同的字符,那么它们对应的整数的与运算的结果等于0。
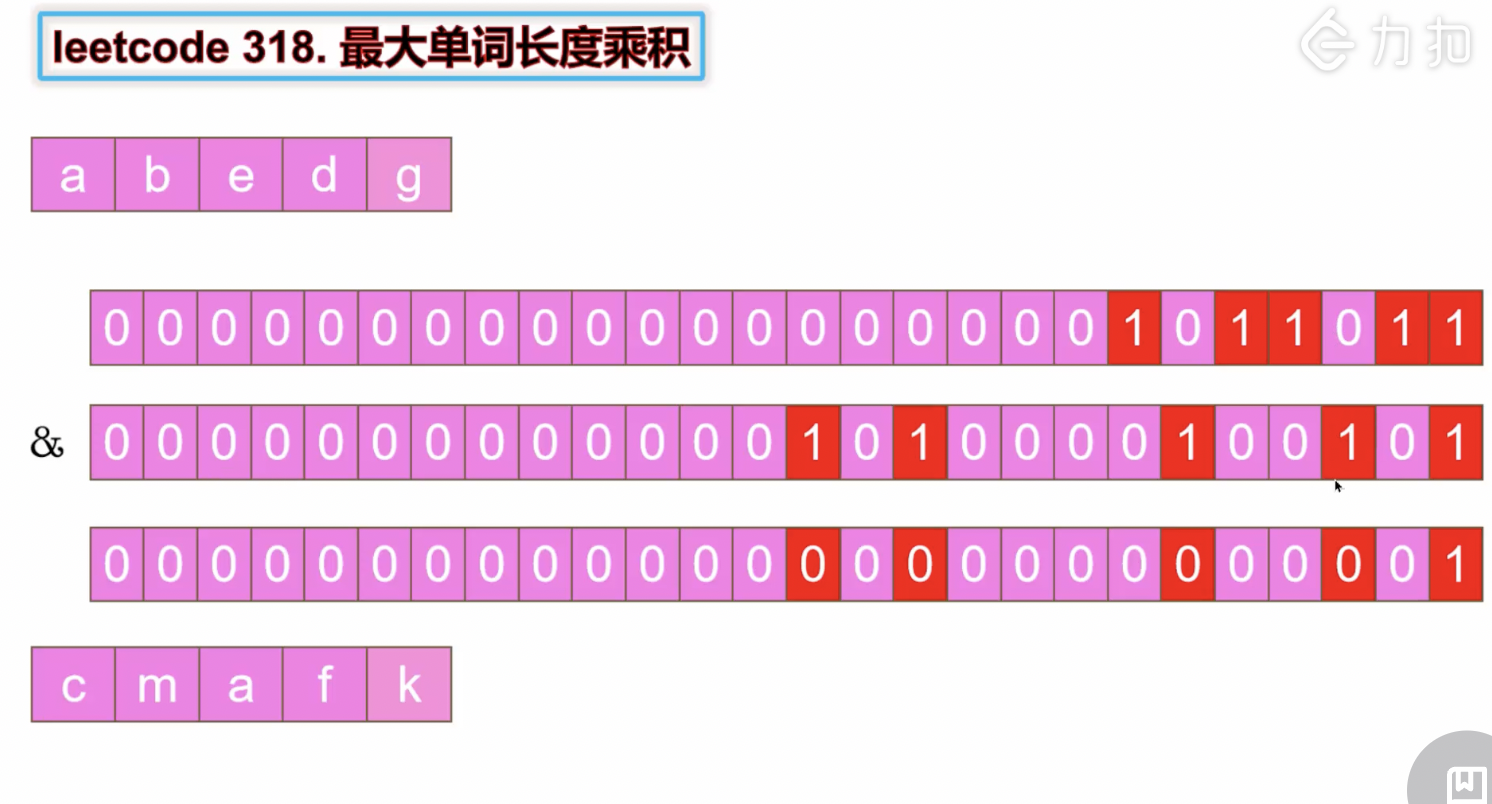
图来源于:https://leetcode-cn.com/problems/aseY1I/solution/jian-dan-yi-dong-javac-pythonjs-zui-da-d-ffga/(讲得很不错)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public int maxProduct(String[] words) {
int[] flags=new int[words.length];
for(int i=0;i<words.length;i++){
for(char ch:words[i].toCharArray()){
// 将1左移ch-'a'位,即将 ch所在位 置为1
// 或操作|等于将所有的赋值连接起来
flags[i] |= 1<<(ch-'a');
}
}
int result=0;
for(int i=0;i<words.length;i++){
for(int j=i+1;j<words.length;j++){
if((flags[i] & flags[j])==0){
int prod=words[i].length()*words[j].length();
result=Math.max(result,prod);
}
}
}
return result;
}
}
|
时间复杂度:O(nk+n^2)(如果数组words的长度为n,平均每个字符串的长度为k)
空间复杂度:O(n)
虽然两种解法的时间复杂度和空间复杂度是同一个量级的,但哈希表的解法在判断两个字符串是否包含相同的字符时,可能需要26次布尔运算,而新的解法只需要1次位运算,因此新的解法的时间效率更高。
使用map优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int maxProduct(vector<string>& words) {
unordered_map<int,int> mp;
for(int i=0;i<words.size();i++){
int bitMask=0;
for(char ch:words[i]){
bitMask |= 1 << (ch-'a');
}
mp[bitMask]=max(mp[bitMask],(int)words[i].length());
}
int result=0;
for(unordered_map<int,int>::iterator it1=mp.begin();it1!=mp.end();it1++){
for(unordered_map<int,int>::iterator it2=mp.begin();it2!=mp.end();it2++){
if((it1->first & it2->first)==0){
result=max(result,mp[it1->first]*mp[it2->first]);
}
}
}
return result;
}
};
|
如果有下列错误:error : no matching function for call to 'max'
将mp[bitMask]=max(mp[bitMask],words[i].length());改为mp[bitMask]=max(mp[bitMask],(int)words[i].length());就行。
这边明显C++的map用起来比较繁琐,所以使用Java改写:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public int maxProduct(String[] words) {
Map<Integer,Integer> map=new HashMap<>();
for(int i=0;i<words.length;i++){
int bitMask=0;
for(char ch:words[i].toCharArray()){
bitMask |= 1 << (ch-'a');
}
map.put(bitMask,Math.max(map.getOrDefault(bitMask,0),words[i].length()));
}
int result=0;
for(int x:map.keySet()){
for(int y:map.keySet()){
if((x & y)==0){
result=Math.max(result,map.get(x)*map.get(y));
}
}
}
return result;
}
}
|
50 Pow(x, n)
求 x^n 最简单的方法是通过循环将 n 个 x 乘起来,时间复杂度为 O(n) 。
快速幂法 可将时间复杂度降低至 O(log n)。
快速幂+递归
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
double quickMul(double x,long long N){
if(N==0) return 1.0;
double y=quickMul(x,N/2);
return N%2==0?y*y:y*y*x;
}
double myPow(double x, int n) {
long long N=n;
return n>=0?quickMul(x,N):1.0/quickMul(x,-N);
}
};
|
-
时间复杂度:O(logn)
-
空间复杂度:O(logn)
快速幂+迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
double quickMul(double x,long long N){
if(N==0) return 1.0;
double res=1.0;
while(N){
if(N&1){
res*=x;
}
x*=x;
N>>=1;
}
return res;
}
double myPow(double x, int n) {
long long N=n;
return n>=0?quickMul(x,N):1.0/quickMul(x,-N);
}
};
|
Author
Anjana
LastMod
2022-01-20
License
原创文章,如需转载请注明作者和出处。谢谢!

