《编程珠玑》的笔记。

Column 2: Aha! Algorithms

三个问题

A.给定一个最多包含40亿个随机排列的32位整数的顺序文件，找出一个不在文件中的32位整数（在文件中至少缺失一个这样的数——为什么？）。

在具有足够内存的情况下，如何解决该问题？

如果有几个外部的“临时”文件可用，但是仅有几百字节的内存，又该如何解决该问题？

输入为顺序文件（考虑磁带或磁盘——虽然磁盘可以随机读写，但是从头至尾读取文件通常会快得多）。文件包含最多40亿个随机排列的32位整数，而我们需要找出一个不存在于该文件中的32位整数。（至少缺少一个整数，因为一共有2^32也就是4 294 967 296个这样的整数。）如果有足够的内存，可以采用第1章中介绍的位图技术，使用536 870 912个8位字节形成位图来表示已看到的整数。

2^32=4,294,967,296

2^32/8=536,870,912

然而，该问题还问到在仅有几百个字节内存和几个稀疏顺序文件的情况下如何找到缺失的整数？为了采用二分搜索技术，就必须定义一个范围、在该范围内表示元素的方式以及用来确定哪一半范围存在缺失整数的探测方法。如何来实现呢？

解答：

我们从表示每个整数的32位的视角来考虑二分搜索。算法的第一趟（最多）读取40亿个输入整数，并把起始位为0的整数写入一个顺序文件，把起始位为1的整数写入另一个顺序文件。

这两个文件中，有一个文件最多包含20亿个整数,我们接下来将该文件用作当前输入并重复探测过程，但这次探测的是第二个位。如果原始的输入文件包含 n个元素，那么第一趟将读取 n 个整数，第二趟最多读取 n/2 个整数，第三趟最多读取n/4个整数，依此类推，所以总的运行时间正比于n。

通过排序文件并扫描，我们也能够找到缺失的整数，但是这样做会导致运行时间正比于nlogn。

B.将一个n元一维向量向左旋转i个位置。例如，当n=8且i=3时，向量abcdefgh旋转为defghabc。简单的代码使用一个n元的中间向量在n步内完成该工作。

能否仅使用数十个额外字节的存储空间，在正比于n的时间内完成向量的旋转?

该问题在应用程序中以各种不同的伪装出现：

• 一些编程语言中，该功能是向量的一个基本操作

• 旋转操作对应于交换相邻的不同大小的内存块：每当拖动文件中的一块文字到其他地方时，就要求程序交换两块内存中的内容

在许多应用场合下，运行时间和存储空间的约束会很严格。

LeetCode类似题：189. Rotate Array

1、使用额外的数组

• 将x的前i个元素复制到一个临时数组中
• 将余下的n－i个元素向左移动i个位置
• 将最初的i个元素从临时数组中复制到x中余下的位置。

2、定义一个函数将x向左旋转一个位置（其时间正比于n）然后调用该函数i次。

该方法产生了过多的运行时间消耗。

3、有限的资源

移动x[0]到临时变量t，然后移动x[i]至x[0]，x[2i]至x[i]，依此类推（将x中的所有下标对n取模），直至返回到取x[0]中的元素，此时改为从t取值然后终止过程。

当i为3且n为12时，元素按如下顺序移动。

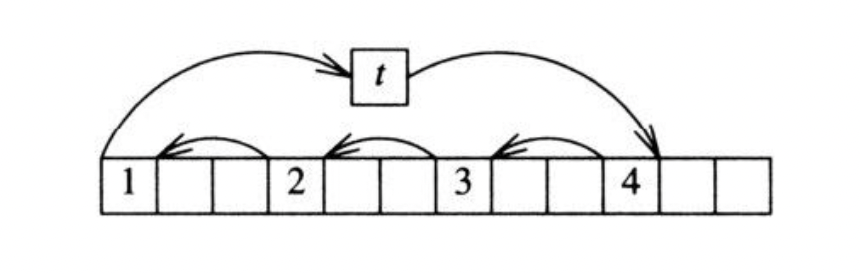
如果该过程没有移动全部元素，就从x[1]开始再次进行移动，直到所有的元素都已经移动为止。

4、

我们将问题看做是把数组ab转换成ba，同时假定我们拥有一个函数可以将数组中特定部分的元素求逆。

作者提到：

Kernighan 报告称在第一次执行的时候程序就正确运行了，而他们先前基于链表的处理相似任务的代码则包含几个错误。该代码用在几个文本处理系统中，其中包括我最初用于录入本章内容的文本编辑器。Ken Thompson在1971年编写了编辑器和这种求逆代码，甚至在那时就主张把该代码当作一种常识。

C.给定一个英语字典，找出其中的所有变位词集合。例如，“pots”、“stop”和“tops”互为变位词，因为每一个单词都可以通过改变其他单词中字母的顺序来得到。

习题

1.考虑查找给定输入单词的所有变位词问题。仅给定单词和字典的情况下，如何解决该问题？

如果有一些时间和空间可以在响应任何查询之前预先处理字典，又会如何？

2.给定包含4 300 000 000个32位整数的顺序文件，如何找出一个出现至少两次的整数？

3.前面涉及了两个需要精巧代码来实现的向量旋转算法。将其分别作为独立的程序实现。在每个程序中，i和n的最大公约数如何出现？

4.几位读者指出，既然所有的三个旋转算法需要的运行时间都正比于n，杂技算法的运行速度显然是求逆算法的两倍。杂技算法对数组中的每个元素仅存储和读取一次，而求逆算法需要两次。在实际的计算机上进行实验以比较两者的速度差异，特别注意内存引用位置附近的问题。